Chybová funkce
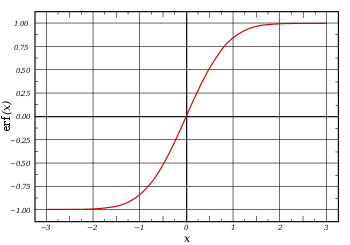
V matematice pojem chybová funkce (také Gaussova chybová funkce) označuje speciální funkci, která není elementární; sigmoidního tvaru; se kterou se lze setkat ve statistice, teorii pravděpodobnosti atd. Je definována jako:
Doplňková chybová funkce, značná erfc, je definována jako:
Imaginární chybová funkce, značená erfi, je definována jako:
Pokud je chybová funkce vypočítána pro libovolný komplexní argument z, pak je výsledná komplexní chybová funkce obvykle brána v omezené formě, jako Krampova funkce:
Externí odkazy[editovat | editovat zdroj]
 Obrázky, zvuky či videa k tématu chybová funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu chybová funkce na Wikimedia Commons





