Levá rekurze

Levá rekurze v teorii formálních jazyků v matematické informatice je speciální případ rekurze, kdy lze určitý neterminální symbol přepsat v jednom nebo více krocích na řetězec, který obsahuje stejný neterminální symbol. O levou rekurzi se jedná, pokud je příslušný neterminál na začátku výsledného řetězce. Lze také říct, že určitý řetězec je rozpoznán jako část jazyka tak, že se skládá z řetězce z téhož jazyka (vlevo) a zbytku, sufixu (vpravo). Například ve výseku gramatiky pro aritmetický výraz: $E\Rightarrow E+T$, $E\Rightarrow T$, $T\Rightarrow konstanta$, je neterminál E zleva rekurzivní. Výraz $1+2+3$ je rozpoznán jako součet, protože jej lze rozložit na součet $1+2$ a sufix ${}+3$.

V termínech bezkontextových gramatik neterminální symbol obsahuje levou rekurzi, jestliže první symbol v jednom z jeho pravidel je samotný (v případě přímé levé rekurze) nebo lze získat řetězec obsahující tentýž symbol nějakou posloupností substitucí (v případě nepřímé levé rekurze).

Definice

Gramatika obsahuje levou rekurzi právě tehdy, když existuje neterminální symbol $A$, ze kterého lze odvodit větnou formu, která začíná původním neterminálem. Symbolicky,

$A\Rightarrow ^{+}A\alpha$,

kde $\Rightarrow ^{+}$ je operace provedení jedné nebo více substitucí a $\alpha$ je libovolný řetězec terminálních a neterminálních symbolů.

Přímá levá rekurze

O přímou levou rekurzi se jedná, když podmínky z definice rekurze jsou splněny již jedinou substitucí. Vyžaduje pravidlo tvaru

$A\to A\alpha$

kde $\alpha$ je řetězec neterminálů a terminálů. Například pravidlo

${\mathit {Expression}}\to {\mathit {Expression}}+{\mathit {Term}}$

je přímo s levou rekurzí. Analyzátor s rekurzivním sestupem zleva doprava pro toto pravidlo může být následující:

funkce Expression()
{
    Expression();  match('+');  Term();
}

Tento kód způsobí při svém provedení nekonečnou rekurzi.

Nepřímá levá rekurze

O nepřímou levou rekurzi se jedná, když jsou podmínky z definice rekurze splněny až při použití více než jednoho přepsání. Má za následek sada pravidel následující vzorek

$A_{0}\to \beta _{0}A_{1}\alpha _{0}$

$A_{1}\to \beta _{1}A_{2}\alpha _{1}$

$\cdots$

$A_{n}\to \beta _{n}A_{0}\alpha _{n}$

kde $\beta _{0},\beta _{1},\ldots ,\beta _{n}$ jsou řetězce, které všechny mohou dávat prázdný řetězec, a $\alpha _{0},\alpha _{1},\ldots ,\alpha _{n}$ jsou libovolné řetězce. Derivace

$A_{0}\Rightarrow \beta _{0}A_{1}\alpha _{0}\Rightarrow ^{+}A_{1}\alpha _{0}\Rightarrow \beta _{1}A_{2}\alpha _{1}\alpha _{0}\Rightarrow ^{+}\cdots \Rightarrow ^{+}A_{0}\alpha _{n}\dots \alpha _{1}\alpha _{0}$

pak dává $A_{0}$ jako první symbol v poslední větné formě.

Odstraňování levé rekurze

Levá rekurze často představuje problém pro analyzátory, buď protože vede k nekonečné rekurzi (v případě většiny analyzátorů shora dolů) anebo protože očekávají pravidla v normální formě, která rekurzi zakazuje (jako v případě mnoha analyzátorů zdola nahoru, včetně CYK algoritmu). Proto se gramatiky často upravují, aby levou rekurzi neobsahovaly.

Odstraňování přímé levé rekurze

Následující algoritmus slouží pro odstranění přímé levé rekurze. Existuje několik jeho vylepšení. Pro každý neterminál $A$ s levou rekurzí, zahodíme všechna pravidla tvaru $A\rightarrow A$ a ostatní pravidla tvaru:

$A\rightarrow A\alpha _{1}\mid \ldots \mid A\alpha _{n}\mid \beta _{1}\mid \ldots \mid \beta _{m}$

kde:

• $\alpha$ jsou neprázdné řetězce neterminálů a terminálů a
• $\beta$ jsou řetězce neterminálů a terminálů, které nezačínají symbolem $A$.

nahradíme dvěma množinami pravidel, jednou se symbolem $A$ na levé straně:

$A\rightarrow \beta _{1}A^{\prime }\mid \ldots \mid \beta _{m}A^{\prime }$

a druhou s přidaným neterminálním symbolem $A'$ (obvykle nazývaným „zakončení“ nebo "zbytek"):

$A^{\prime }\rightarrow \alpha _{1}A^{\prime }\mid \ldots \mid \alpha _{n}A^{\prime }\mid \epsilon$

Uvedený postup se opakuje, dokud nezůstává žádná přímá levá rekurze.

Jako příklad uvažujme sadu pravidel

${\mathit {Expression}}\rightarrow {\mathit {Expression}}+{\mathit {Expression}}\mid {\mathit {Integer}}\mid {\mathit {Retezec}}$

kterou lze přepsat, aby se zabránilo levé rekurzi jako

${\mathit {Expression}}\rightarrow {\mathit {Integer}}\,{\mathit {Expression}}'\mid {\mathit {Retezec}}\,{\mathit {Expression}}'$

${\mathit {Expression}}'\rightarrow {}+{\mathit {Expression}}\,{\mathit {Expression}}'\mid \epsilon$

Odstraňování veškeré levé rekurze

Topologickým setříděním neterminálů lze výše uvedený postup rozšířit na odstraňování nepřímé levé rekurze:

Vstup Gramatika: množina neterminálů $A_{1},\ldots ,A_{n}$ a jejich pravidel

Výstup Upravená gramatika generující stejný jazyk, ale bez levé rekurze

1. Pro každý neterminál $A_{i}$:
   1. Opakuj, dokud iterace mění gramatiku:
      1. Pro každé pravidlo $A_{i}\rightarrow \alpha _{i}$, $\alpha _{i}$ je řetězec terminálů a neterminálů:
         1. Jestliže $\alpha _{i}$ začíná neterminálem $A_{j}$ a $j<i$:
            1. Nechť $\beta _{i}$ jsou $\alpha _{i}$ bez jeho úvodní $A_{j}$.
            2. Odstraň pravidlo $A_{i}\rightarrow \alpha _{i}$.
            3. Pro každé pravidlo $A_{j}\rightarrow \alpha _{j}$:
               1. Přidej pravidlo $A_{i}\rightarrow \alpha _{j}\beta _{i}$.
   2. Odstraň přímou levou rekurzi pro $A_{i}$, jak je popsáno výše.

Všimněte si, že tento algoritmus je velmi citlivý na pořadí neterminálů; jeho optimalizace se často zaměřují na správný výběr tohoto řazení.

Skryté nástrahy

Ačkoli výše uvedené transformace nemění generovaný jazyk, mohou měnit derivační strom, na kterém závisí struktura řetězce. Existují postupy, které pomocí stromových transformací mohou vést k původním výsledkům. Při vynechání tohoto kroku však rozdíly mohou změnit sémantiku analýzy.

Obzvláště zranitelná je asociativita; zleva asociativní operátory jsou do nové gramatiky převedeny jako zprava asociativní. Pokud například uvažujeme následující gramatiku:

${\mathit {Expression}}\rightarrow {\mathit {Expression}}\,-\,{\mathit {Term}}\mid {\mathit {Term}}$

${\mathit {Term}}\rightarrow {\mathit {Term}}\,*\,{\mathit {Factor}}\mid {\mathit {Factor}}$

${\mathit {Factor}}\rightarrow ({\mathit {Expression}})\mid {\mathit {Integer}}$

standardní transformace pro odstranění levé rekurze dává následující:

${\mathit {Expression}}\rightarrow {\mathit {Term}}\ {\mathit {Expression}}'$

${\mathit {Expression}}'\rightarrow {}-{\mathit {Term}}\ {\mathit {Expression}}'\mid \epsilon$

${\mathit {Term}}\rightarrow {\mathit {Factor}}\ {\mathit {Term}}'$

${\mathit {Term}}'\rightarrow {}*{\mathit {Factor}}\ {\mathit {Term}}'\mid \epsilon$

${\mathit {Factor}}\rightarrow ({\mathit {Expression}})\mid {\mathit {Integer}}$

Syntaktická analýza řetězce „1 - 2 - 3“ LALR analyzátorem podle původní gramatiky (LALR analyzátor umožňuje analýzu gramatik s levou rekurzí) dává derivační strom:

Analýza opakovaného odčítání s levou rekurzí

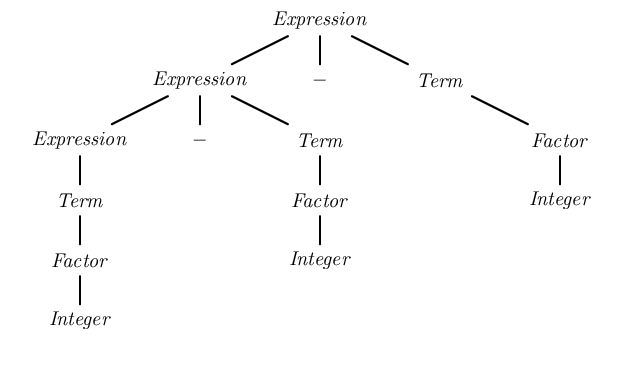
Tento derivační strom seskupuje termy odleva, což dává správnou sémantiku (1 - 2) - 3.

Syntaktická analýza podle upravené gramatiky dává derivační strom

Analýza opakovaného odčítání obsahující pravou rekurzi

,

který je při správné interpretaci 1 + (-2 + (-3)) také správný, ale méně věrný vstupu, a implementace některých operátorů může být mnohem obtížnější. Všimněte si, že se termy vpravo vyskytují hlouběji ve stromě, podobně jako v gramatice s pravou rekurzí jejich úpravou na 1 - (2 - 3).

Ošetření levé rekurze při analýze shora dolů

Formální gramatika, která obsahuje levou rekurzi, nemůže být analyzována LL(k)-analyzátorem nebo jiným naivním analyzátorem s rekurzivním sestupem, pokud není zkonvertována na tvar slabě ekvivalentní gramatiky s pravou rekurzí. Naproti tomu, levá rekurze je upřednostňovaná pro LALR analyzátory, protože vede k menšímu využívání zásobníku než pravá rekurze. Rafinovanější analyzátory shora dolů však mohou implementovat obecné bezkontextové gramatiky pomocí omezení. V roce 2006 popsali Frost a Hafiz algoritmus, který je použitelný pro nejednoznačné gramatiky s přímou levou rekurzí. Tento algoritmus v roce 2007 rozšířil Frost, Hafiz a Callaghan na úplný algoritmus analýzy, který dovoluje nepřímou i přímou levou rekurzi v polynomiálním čase a pro vysoce nejednoznačné gramatiky generuje kompaktní reprezentaci polynomiální velikosti pro potenciálně exponenciální funkci počtu stromů analýzy. Autoři pak implementovali algoritmus jako sadu kombinátorů syntaktických analyzátorů napsaný v jazyce Haskell.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Left recursion na anglické Wikipedii.

Související články

• Koncová rekurze

Externí odkazy

• CMU lecture on left recursion Archivováno 3. 3. 2016 na Wayback Machine.
• Practical Considerations for LALR(1) Grammars
• X-SAIGA – eXecutable SpecificAtIons of GrAmmars