Binární halda
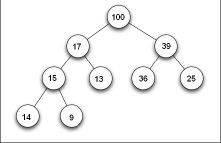

Binární halda je obzvláště jednoduchý typ datové struktury halda, která je vytvořená použitím binárního stromu. Můžeme si jej představit jako binární strom se dvěma dalšími omezeními.
- Vlastnost tvaru – strom je buď perfektně vyvážený binární strom (všechny listy jsou ve stejné úrovni), nebo pokud je poslední úroveň stromu nekompletní, uzly plní strom zleva doprava.
- Vlastnost haldy - každý uzel je větší nebo roven všem svým potomkům
„Větší než“ je chápáno ve smyslu porovnávací funkce zvolené k uspořádání haldy, nemusí se nutně jednat o „větší než“ v matematickém významu (nejedná se vždy o číselné hodnoty). Haldy, kde porovnávací funkcí je matematické „větší než“, jsou zvané max-haldy. Tam kde porovnávací funkcí je matematické „menší než“, jedná se o min-haldu. Častější jsou min-haldy, které lze jednoduše použít v prioritních frontách.
Všimněte si, že pořadí sourozenců v haldě není v jejích vlastnostech určeno. Dva potomky téhož rodiče lze volně vyměnit (pokud to neporušuje vlastnosti haldy, porovnejte s binárním vyhledávacím stromem).
Operace s haldou[editovat | editovat zdroj]
Vkládání do haldy[editovat | editovat zdroj]
Pokud chceme přidat prvek do existující haldy, lze vykonat operaci známou jako up-heap, buble-up, percolate-up, nebo sift-up. Tyto funkce slouží k obnovení vlastností haldy. Při použití binární haldy to lze provést v čase pomocí následujícího algoritmu:
- přidáme prvek na spodní úroveň haldy
- porovnáme přidaný prvek s jeho rodičem, pokud je ve správném vztahu, tak skončíme
- pokud ne, prohodíme prvek s rodičem a zopakujeme předešlý krok
Počet kroků je maximálně roven počtu úrovní ve stromě – hloubce stromu, která je O(log n). Nicméně přibližně 50% prvků jsou listy a 75% prvků haldy se nachází ve spodních dvou úrovních. Je tedy pravděpodobné, že nově vkládaný prvek se přesune jen o pár úrovní nahoru, aby halda zůstala zachována. Binární halda proto podporuje vkládání v průměrném konstantním čase O(1).
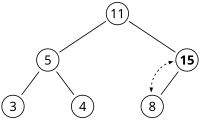
Řekněme, že máme haldu
a chceme do ní přidat číslo 15. Nejprve umístíme 15 na pozici označenou X. Avšak vlastnost haldy je porušena protože 15 je větší než 8, proto musíme prohodit 15 a 8. Zde je obrázek haldy jako po prvním přesunu:
Ale vlastnosti haldy jsou stále porušeny, 15 je větší než 11, tedy potřebujeme další přesun:
Nyní jsme již získali validní max-haldu.
Smazání kořene z haldy[editovat | editovat zdroj]
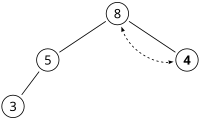
Procedura pro mazání kořene z haldy – vlastně odebíraní maximálního prvku z max-haldy nebo minimálního prvku z min-haldy - začíná výměnou kořene za poslední prvek v poslední úrovni. Takže, máme-li max-haldu z prvního obrázku, odebereme 11 a nahradíme ji 4.
Nyní je vlastnost haldy porušena, protože 8 je větší než 4. Operace, která obnoví vlastnosti haldy, se nazývá down-heap, bubble-down, percolate-down nebo sift-down. V tomto případě stačí výměna dvou prvků 4 a 8 k obnovení vlastností haldy a již nepotřebujeme prohazovat další prvky.
Obecně, nesprávný uzel je prohozen s jeho větším potomkem v max-haldě (v min-haldě by měla být výměna s menším potomkem), dokud nejsou splněny vlastnosti haldy. Všimněte si, že down-heap operaci (bez předcházející výměny) lze obecně použít ke změně hodnoty kořene, i když žádný prvek nebyl smazán.
Složitost operací[editovat | editovat zdroj]
| Operace | Složitost |
|---|---|
| Stavba haldy | O(n) |
| Získání hodnoty kořene | O(1) |
| Vyjmutí kořene | O(log n) |
| Vložení prvku | O(log n) |
| Odstranění prvku | O(log n) |
| Sloučení 2 hald | O(n1 + n2) |
n = počet prvků, n1 = počet prvků 1. haldy, n2 = počet prvků 2. haldy
Z důvodu neefektivní operace sloučení dvou hald se závadějí binomiální a Fibonacciho haldy.
Stavba haldy[editovat | editovat zdroj]
Tato procedura sestavuje haldu z pole. Jinými slovy přerovnává prvky pole tak, aby pole mělo vlastnosti haldy. Začíná se pracovat od středu pole. Časová náročnost tohoto algoritmu je při implementaci haldy založené na poli, kde je počet uzlů v haldě. Většina změn (označovaných jako heapify) se provádí, když má halda malou výšku, proto má operace menší časovou náročnost, než by se zdálo.
Konkrétně heapify zaberou času, kde h je nynější výška haldy. Počet uzlů ve výšce h je . Proto celková cena heapify činí
Implementace haldy[editovat | editovat zdroj]
K implementaci binární haldy je možné použít datové struktury binárního stromu. Je zde problém s hledáním sousedního prvku v poslední úrovni při přidávání prvku, což lze řešit algoritmicky nebo přidáním dodatečných dat do uzlů, čemuž se říká „threading“ (zřetězení) – kromě odkazů na potomky ukládáme také odkaz na následující uzel.

Obvyklejším přístupem, který také odpovídá teorii stojící za haldou, je uložení haldy do pole. Každý binární strom může být uložen v poli, ale protože halda je vždy skoro kompletní binární strom, může být uložen kompaktně/pevně. Není nutný žádný prostor pro ukazatele, místo toho rodič a potomek každého uzlu mohou být nalezeni jednoduchou aritmetikou v indexovaném poli. Detaily závisí na pozici kořene (který zase závisí na omezení programovacího jazyka použitého pro implementaci). Pokud má kořen stromu index ( je počet prvků stromu, které jsou a[0].a[n−1]), potom pro každý index má prvek potomky a , a rodiče a[floor((i−1)/2)], jak ukazuje obrázek. Pokud je kořen (prvky stromu jsou ), pak prvek má potomky a , a rodiče je . Toto je jednoduchý příklad implicitní datové struktury.
Tento přístup je obzvláště užitečný v algoritmu heapsort, kde umožňuje využít prostor ve vstupním poli k opětovnému uložení haldy. Nicméně vyžaduje alokaci pole před naplněním, což dělá tuto metodu ne tak použitelnou pro implementaci prioritní fronty, kde počet úloh (prvků haldy) nemusí být znám předem.
Operace unheap/downheap lze v podmínkách pole provést následovně: předpokládejme, že vlastnosti haldy platí pro indexy . Funkce sift-down rozšiřuje vlastnosti haldy na . Jen index porušuje vlastnosti haldy. Nechť je index největšího potomka (pro max-haldu, nebo nejmenšího potomka pro min-haldu), v rozsahu . (Jestliže takový index neexistuje, protože , potom vlastnost haldy platí pro nově rozšířený rozsah a není třeba nic dělat.) Přehozením hodnot a je dodržena vlastnost haldy pro index . V tomto bodě je jediným problémem, že vlastnost haldy nemusí platit pro index . Funkce sift-down je aplikována rekurzivně na index dokud nebude vlastnost haldy dodržena pro všechny prvky.
Funkce sift-down je rychlá. V každém kroku potřebuje jen dvě porovnání a jednu výměnu. Hodnota indexu, kde pracuje, se zdvojnásobí v každé iteraci, takže je nutno provést nanejvýš kroků.
Spojovací operace v binární haldě spotřebuje Θ(n) pro stejně setříděné haldy. Pokud je spojení prováděno často, doporučuje se jiná implementace haldy, jako třeba binomiální halda.
Odkazy[editovat | editovat zdroj]
Literatura[editovat | editovat zdroj]
- MAREŠ, Martin; VALLA, Tomáš. Průvodce labyrintem algoritmů. Praha: CZ.NIC, 2017. Dostupné online. ISBN 978-80-88168-19-5. Kapitola 4.2 Datové struktury – Haldy.












![{\displaystyle a[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1044e76c899aeac9739cf7ba3e1a477063f06c9d)
![{\displaystyle a[2i+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e6faa4e543a0eb66c99cc7824c6b6a8f3816de3)
![{\displaystyle a[2i+2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e80b26b8d0173a987308e3102ec8bd89bda949cb)
![{\displaystyle a[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06bee2e44d2a2734982592d8d9eb754ecd5588fc)
![{\displaystyle a[1]..a[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b89c80ce0210dd876164e97281fd83ecce1e764a)
![{\displaystyle a[2i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f285f6c705d31eee298b383d3dfde9fedb3b6ea)
![{\displaystyle a[floor(i/2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2752ff376705890054923fc8c90d7b7b2bbb625)






![{\displaystyle a[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8acb1137a37491514f15dd5d7b6aebfb0209ccc)
