UPGMA

UPGMA (unweighted pair group method with arithmetic mean; česky metoda neváženého párování s aritmetickým průměrem) je jednoduchá aglomerativní hierarchická shluková metoda (jde o tzv. bottom-up metodu, kdy se nejprve shlukují páry sobě nejpodobnější, které se následně shlukují až do konečné sítě). Metodu představili Sokal a Michener.

Termín nevážená metoda nesouvisí s matematickým výpočtem, ale odkazuje na skutečnost, že všechny distance se podílejí stejnou měrou na výpočtu každého průměru. Metoda UPGMA má i alternativu váženého párování, která se nazývá WPGMA. WPGMA generuje výsledky na základně jednoduchého průměru vzdáleností (neboli distancí), zatímco u nevážené metody UPGMA se používá k výpočtu proporcionální průměr (viz pracovní příklad).

Algoritmus

Algoritmus UPGMA vytváří zakořeněný strom (tzv. dendrogram), který odráží strukturu matice podobností (nebo matice odlišností). V každém kroku jsou dva nejpodobnější klastry sloučeny do klastru vyšší úrovně. Vzdálenost mezi každými dvěma klastry ${\mathcal {A}}$ a ${\mathcal {B}}$ o velikosti (neboli mohutnosti) ${|{\mathcal {A}}|}$ a ${|{\mathcal {B}}|}$ je vypočítána jako průměr všech vzdáleností $d(x,y)$ mezi páry prvků $x$ v ${\mathcal {A}}$ a $y$ v ${\mathcal {B}}$, tzn. jako střední vzdálenost mezi prvky každého klastru:

${1 \over {|{\mathcal {A}}|\cdot |{\mathcal {B}}|}}\sum _{x\in {\mathcal {A}}}\sum _{y\in {\mathcal {B}}}d(x,y)$

Jinými slovy, v každém kroku se aktualizuje vzdálenost mezi nově spojenými klastry ${\mathcal {A}}\cup {\mathcal {B}}$ a novým clustrem $X$. Aktualizovaná vzdálenost je dána proporcionálním průměrem vzdáleností $d_{{\mathcal {A}},X}$ a $d_{{\mathcal {B}},X}$:

$d_{({\mathcal {A}}\cup {\mathcal {B}}),X}={\frac {|{\mathcal {A}}|\cdot d_{{\mathcal {A}},X}+|{\mathcal {B}}|\cdot d_{{\mathcal {B}},X}}{|{\mathcal {A}}|+|{\mathcal {B}}|}}$

Algoritmus UPGMA vytváří zakořeněné dendrogramy, při jejichž tvorbě předpokládá konstantní podíly - to znamená, že předpokládá tzv. ultrametrický strom, ve kterém jsou vzdálenosti od kořene ke konci každé větve stejné. Pokud jsou základem pro tvorbu stromu molekulární data (tj. DNA, RNA nebo proteiny) odebraná ve stejný čas, ultrametricita se stane ekvivalentem molekulárních hodin.

Pracovní příklad

Tento pracovní příklad je založen na matici genetických distancí JC69, která je odvozená z alignmentu sekvencí 5S ribozomální RNA pěti bakterií: Bacillus subtilis ($a$), Bacillus stearothermophilus ($b$), Lactobacillus viridescens ($c$), Acholeplasma modicum ($d$) a Micrococcus luteus ($e$).

První krok

• První shlukování (klastrování)

Předpokládejme, že máme pět prvků $(a,b,c,d,e)$ uspořádaných v následující matici párových vzdáleností $D_{1}$:

	a	b	c	d	e
a	0	17	21	31	23
b	17	0	30	34	21
c	21	30	0	28	39
d	31	34	28	0	43
e	23	21	39	43	0

Protože je v této matici je nejmenší hodnotou $D_{1}(a,b)=17$, v prvním kroku spojíme prvky $a$ a $b$.

• Odhad délky první větve

Písmenem $u$ označme uzel, ve kterém se nyní spojují prvky $a$ a $b$. Díky rovnici $\delta (a,u)=\delta (b,u)=D_{1}(a,b)/2$ je zajištěno, že prvky $a$ a $b$ jsou stejně vzdálené od $u$. To odpovídá hypotéze ultrametricity. Větve obou prvků $a$ a $b$ vedoucí k uzlu $u$ tedy mají délku $\delta (a,u)=\delta (b,u)=17/2=8.5$ (viz výsledný dendrogram).

• První aktualizace matice vzdáleností

Poté přistoupíme k aktualizaci počáteční matice $D_{1}$ na novou matici $D_{2}$ (viz níže), která bude zmenšená o jeden řádek a jeden sloupec kvůli seskupování $a$ s $b$ v předchozím kroku. Nové hodnoty vzdáleností odpovídají průměru vzdáleností mezi každým prvkem prvního klastru $(a,b)$ a každým ze zbývajících prvků:

$D_{2}((a,b),c)=(D_{1}(a,c)\times 1+D_{1}(b,c)\times 1)/(1+1)=(21+30)/2=25.5$

$D_{2}((a,b),d)=(D_{1}(a,d)+D_{1}(b,d))/2=(31+34)/2=32.5$

$D_{2}((a,b),e)=(D_{1}(a,e)+D_{1}(b,e))/2=(23+21)/2=22$

Nově vypočtené hodnoty vzdáleností v matici $D_{2}$ jsou vyznačeny tučně. Hodnoty psané kurzívou v matici $D_{2}$ nebyly změněny oproti původní matici $D_{1}$, protože jde o vzdálenosti mezi prvky, které nebyly zahrnuty do prvního klastru.

Druhý krok

• Druhé shlukování

Nyní zopakujeme tři předchozí kroky, počínaje tvorbou nové matice vzdálenosti $D_{2}$

	(a, b)	c	d	e
(a, b)	0	25.5	32.5	22
c	25.5	0	28	39
d	32.5	28	0	43
e	22	39	43	0

V této matici je nejmenší hodnotou $D_{2}((a,b),e)=22$, proto ke klastru $(a,b)$ připojíme prvek $e$.

• Odhad délky druhé větve

Označme uzel spojující klastr $(a,b)$ a prvek $e$ písmenem $v$. Kvůli ultrametricitě musí mít větve spojující klastr ($a$, $b$) a $e$ v uzlu $v$ stejnou délku: $\delta (a,v)=\delta (b,v)=\delta (e,v)=22/2=11$

Délku nové větve vypočteme následovně: $\delta (u,v)=\delta (e,v)-\delta (a,u)=\delta (e,v)-\delta (b,u)=11-8.5=2.5$ (viz výsledný dendrogram)

• Druhá aktualizace matice vzdáleností

Poté přistoupíme k aktualizaci matice $D_{2}$ na novou distanční matici $D_{3}$ (viz níže), zmenšenou o jeden řádek a jeden sloupec kvůli vzniku nového klastru $(a,b)$ a $e$. Tučně zvýrazněné hodnoty v $D_{3}$ odpovídají novým vzdálenostem, vypočteným na základně proporcionálního průměru:

$D_{3}(((a,b),e),c)=(D_{2}((a,b),c)\times 2+D_{2}(e,c)\times 1)/(2+1)=(25.5\times 2+39\times 1)/3=30$

Výpočet nové vzdálenosti pomocí proporcionálního průměru umožňuje vzít v potaz větší velikost klastru $(a,b$ - dva prvky) s ohledem na $e$ (jeden prvek). Podobně vypočteme zbývající vzdálenost:

$D_{3}(((a,b),e),d)=(D_{2}((a,b),d)\times 2+D_{2}(e,d)\times 1)/(2+1)=(32.5\times 2+43\times 1)/3=36$

Proporcionální průměr tedy dává stejnou váhu všem počátečním vzdálenostem matice $D_{1}$. To je důvod, proč je metoda nevážená - ne s ohledem na matematický postup, ale s ohledem na počáteční vzdálenosti.

Třetí krok

• Třetí shlukování

Znovu zopakujeme tři předchozí kroky, přičemž nejprve vytvoříme novou matici vzdáleností $D_{3}$.

	((a, b), e)	c	d
((a, b), e)	0	30	36
c	30	0	28
d	36	28	0

Nejmenší hodnotou této matice je $D_{3}(c,d)=28$, takže spojíme prvky $c$ a $d$ .

• Odhad délky třetí větve

Písmenem $w$ označme uzel, který spojuje prvky $c$ a $d$. Větve spojující $c$ a $d$ v uzlu $w$ pak mají délku $\delta (c,w)=\delta (d,w)=28/2=14$ (viz výsledný dendrogram)

• Třetí aktualizace matice vzdáleností

Nyní je třeba aktualizovat jen jednu hodnotu, přičemž je třeba mít na paměti, že každý z prvků $c$ a $d$ přispívají k výpočtu průměru hodnotou $1$:

$D_{4}((c,d),((a,b),e))=(D_{3}(c,((a,b),e))\times 1+D_{3}(d,((a,b),e))\times 1)/(1+1)=(30\times 1+36\times 1)/2=33$

Poslední krok

Finální matice $D_{4}$ je následující:

	((a, b), e)	(c,d)
((a, b), e)	0	33
(c,d)	33	0

Spojili jsme tudíž oba klastry $((a,b),e)$ a $(c,d)$.

Písmenem $r$ označme (kořenový) uzel, ve kterém spojíme klastry $((a,b),e)$ a $(c,d)$. Větve klastrů $((a,b),e)$ a $(c,d)$ vedoucí k uzlu $r$ pak mají délky:

$\delta (((a,b),e),r)=\delta ((c,d),r)=33/2=16.5$

Vypočteme délky dvou zbývajících větví:

$\delta (v,r)=\delta (((a,b),e),r)-\delta (e,v)=16.5-11=5.5$

$\delta (w,r)=\delta ((c,d),r)-\delta (c,w)=16.5-14=2.5$

Výsledný dendrogram UPGMA

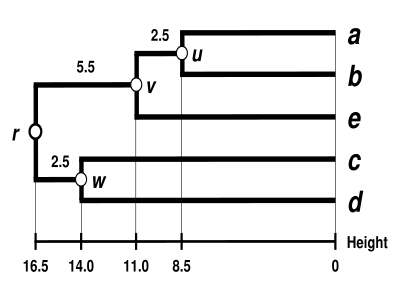
Dendrogram je nyní dokončen. Je ultrametrický, protože všechny konce větví (od $a$ po $e$) jsou stejně vzdálené od uzlu $r$:

$\delta (a,r)=\delta (b,r)=\delta (e,r)=\delta (c,r)=\delta (d,r)=16.5$

Dendrogram je proto zakořeněn nejhlubším uzlem $r$, který je nazýván kořen.

Porovnání s jinými algoritmy

Alternativní klastrovací schémata zahrnují single linkage clustering (metoda nejbližšího souseda, jednospojná metoda), complete linkage clustering (metoda nejvzdálenějšího souseda, všespojná metoda) a WPGMA. Jednotlivé algoritmy se mezi sebou liší použitím jiných postupů při výpočtu vzdáleností mezi klastry v rámci tvorby nové matice. Nevýhodou nejjednodušší metody single linkage clustering je tzv. chaining phenomenon, při kterém dochází ke shlukování klastrů na základě jediného společného charakteru přestože jsou si jednotlivé prvky v klastru obecně nepodobné. Algoritmus Complete linkage clustering dokáže tuto nevýhodu řešit a tvoří klastry o přibližně stejných diametrech.

Porovnání dendrogramů získaných různými shlukovacími metodami na základě stejné distanční matice .

Single-linkage clustering	Complete-linkage clustering	Average linkage clustering: WPGMA	Average linkage clustering: UPGMA

Použití

• Jde o jednu z nejpopulárnějších metod v ekologii. Požívá se pro klasifikaci vzorků (jako jsou např. vegetační snímky) na základě párových podobností jejich vlastností (jako je např. druhové složení). Mimo vegetační data může sloužit také například k pochopení trofické interakce mezi mořskými bakteriemi a protisty.
• V bioinformatice se UPGMA používá k tvorbě fenetických stromů (fenogramů). Metoda UPGMA byla původně navržena pro studie založené na proteinové elektroforéze, ale v současné době se nejčastěji používá k výpočtu vodících stromů pro sofistikovanější algoritmy. Tento algoritmus se používá například při výpočtu alignmentu sekvencí, kdy se na jeho základě tvoří pořadí, ve kterém budou sekvence alignovány. Vodící strom založený na UPGMA seskupuje nejpodobnějších sekvencí bez ohledu na jejich evoluční vývoj nebo fylogenetickou afinitu.
• Při použití metody UPGMA ve fylogenetice se předpokládá konstantní rychlost evoluce (tzv. hypotéza molekulárních hodin) a že všechny vzorky byly odebrány současně. Nicméně se nepovažuje za vhodnou metodu pro odvozování fylogenetických vztahů. Metodu lze použít pouze pokud byly zmíněné předpoklady testovány a dobře zdůvodněny. Je důležité si uvědomit, že strom vytvořený na základě vzorků odebraných v různých časech by neměl vést k ultrametrickému stromu, dokonce i za podmínky „strict clock“.

Časová složitost

Základní použití UPGMA algoritmu ke konstrukci stromu má časovou komplexitu $O(n^{3})$. Pokud použijeme pro každý klastr haldu, abychom jednotlivé klastry udželi ve vzdálenosti od ostatních, redukujeme čas na $O(n^{2}\log n)$. Fionn Murtagh představil nějaké další přístupy pro speciální případy: časový algoritmus $O(k3^{k}n^{2})$ podle Day a Edelsbrunner pro k-dimensionální data, kde je optimální $O(n^{2})$ pro konstantní k, a další algoritmus $O(n^{2})$ pro omezené vstupy, pokud „shlukovací strategie vyhovuje reducibilitě“.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku UPGMA na anglické Wikipedii.

Související články

• Shluková analýza
• Hierarchické seskupování
• Molekulární hodiny

Externí odkazy

• Implementace klastrovacího algoritmu UPGMA v Ruby (AI4R)
• Příklad výpočtu UPGMA pomocí matice podobnosti
• Příklad výpočtu UPGMA pomocí distanční matice