Ekvalizace histogramu
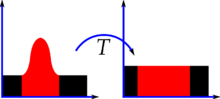
Ekvalizace histogramu je metoda upravující kontrast rastrového obrazu s využitím jeho histogramu (sloupkového diagramu).
Metoda obvykle zvyšuje lokální kontrast rastrových obrázků, zejména když jsou použitá obrazová data reprezentována blízkými hodnotami. Díky těmto úpravám intenzity mohou být jednotlivé jasové hodnoty v histogramu lépe rozloženy. Tyto změny umožňují získat v obrazu větší kontrast.
Metoda je užitečná pro obrazy, které jsou buď příliš tmavé, nebo příliš světlé. Ekvalizace histogramu může vést ke zřetelnějšímu znázornění struktur u rentgenových snímků kostí a ke zvýraznění detailů fotografií, které jsou podexponované nebo přeexponované. Hlavní výhoda této operace je, že je poměrně jednoduchá a současně invertibilní (jestliže známe funkci ekvalizace histogramu, pak můžeme obnovit původní obrázek). Výpočet není nikterak výpočetně náročný. Nevýhodou metody je to, že je nerozlišující, což znamená, že může zvětšit kontrast šumu v pozadí, zatímco se sníží užitečný signál.
Zdá se, že ekvalizaci histogramu využívají i biologické nervové sítě. To bylo konkrétně pozorováno a dokázáno u oka mouchy.
Implementace[editovat | editovat zdroj]
Mějme rastrový obraz ve stupních šedi a nechť jako počet výskytů úrovně šedé . Pravděpodobnost výskytu bodu úrovně šedé v obrazu pak je:
- ,
kde je celkový počet různých úrovní šedi v obrazu, celkový počet bodů v obrazu. Pak je vlastně sloupcový diagram normalizovaný do intervalu .
Definujme jako kumulativní distributivní funkci odpovídající :
- .
Nyní chceme definovat transformaci hodnot pixelů ve formě tak, aby kumulativní distributivní funkce byla ve svém oboru hodnot linearizována. Tato transformace je definována:
Víme, že T mapuje úrovně šedi do intervalu . Abychom vrátili hodnoty do jejich původní oblasti, musíme na výsledek aplikovat následující jednoduchou transformaci:
Popsali jsme vyrovnání histogramu na obrazu ve stupních šedi. Metoda může být použita i na barevné obrazy. Vhodné je ale nejprve převést obraz do barevného modelu YIQ (vyrovnání histogramu pak aplikujeme na kanál Y) nebo HSV.
Malý obraz (8 krát 8 pixelů)[editovat | editovat zdroj]
 |
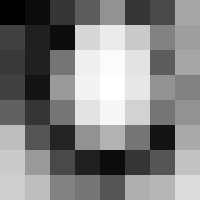 |
Obrázek v plné velikosti[editovat | editovat zdroj]
 |
 |
 |
 |
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
V tomto článku byl použit překlad textu z článku Histogram equalization na anglické Wikipedii.







![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)





