Wikipedista:Kubajzz/odkladiste

Pojmem slapové jevy (také nazývané dmutí) se rozumí cyklické zvyšování a snižování (příliv a odliv) hladiny oceánů a moří způsobené slapovými silami Slunce a Měsíce. Slapové jevy mění hloubky moří a přilehlých vodních těles včetně řek, způsobují oscilující mořské proudy a vytvářejí přílivové pásmo (pruh pobřeží, který je zaplavený při přílivu a odkrytý při odlivu), významné z ekologického hlediska.
Charakteristika přílivu či odlivu závisí na postavení Slunce a Měsíce, povaze pobřeží a dna a může být silně ovlivněna větrem. Obecně existují i jiné slapové jevy než příliv a odliv a nastat mohou kdekoliv, kde se gravitační pole mění v čase a prostoru (viz Jiné slapové jevy).
Charakteristika[editovat | editovat zdroj]
Slapové jevy jsou důsledkem deformace povrchu oceánu vlivem sil kterými na vodní masu působí nebeská tělesa, v případě Země především Měsíce a Slunce. Teoreticky mohou slapové síly dokonce způsobit rozpad obíhajícího tělesa pokud oběžná vzdálenost je nižší než tzv. Rocheova mez.
Opakující se cyklus se skládá z následujících fází:
- Voda stoupá po několik hodin, nastává příliv
- Hladina vody dosáhne maxima, nastane vrchol přílivu a proud vody se pomalu otáčí
- Několik hodin hladina vody klesá, probíhá odliv
- Hladina klesne na minimum, nastává vrchol odlivu a proud vody se pomalu otáčí zpět
Skočný a hluchý příliv[editovat | editovat zdroj]
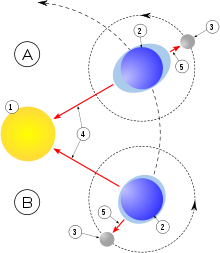
Půldenní rozsah změny hladiny (rozdíl mezi vrcholem odlivu a vrcholem přílivu během půl dne) se mění ve dvoutýdenních cyklech v návaznosti na fáze měsíce. Kolem úplňku a novu, kdy se Slunce, Země a Měsíc nacházejí přibližně v přímce, se síly Slunce a Měsíce sčítají a rozsah dmutí dosahuje maxima; takový příliv se nazývá skočný. Pokud je Měsíc v první čtvrti či poslední čtvrti, svírá se Sluncem úhel kolem 90° a vliv Slunce oslabuje vliv Měsíce; rozsah dmutí je minimální a příliv se nazývá hluchý. Mezi hluchým a skočným přílivem je vždy interval přibližně 7 dní.
Na rozsah dmutí má také vliv vzdálenost Měsíce od Země, která kolísá zhruba o 8%[1]. Je li Měsíc v perigeu (nejblíže Zemi), rozsah dmutí se mírně zvyšuje, je-li v apogeu (nejdále od Země), rozsah dmutí je utlumen. Když se doba perigea shodne s dobou skočného přílivu, je příliv ještě zesílen, naopak pokud nastane hluchý příliv ve chvíli apogea, dojde k maximálnímu možnému utlumení dmutí.
Lokální charakteristika[editovat | editovat zdroj]


Aktuální fáze dmutí v daném místé záleží na mnoha faktorech. Místa na zemi, kde se hladina oceánu vždy nachází ve stejné fázi, je možné spojit čárami stejného vodního stavu. Kdyby na Zemi nebyly pevniny a oceánské dno bylo všude stejně rovné, tyto čáry by kopírovaly směr poledníků. Ve skutečnosti ale v oceánu ohraničeném okruhem pevniny směřují čáry od břehů ke středu, kde se nachází místo s nulovou amplitudou dmutí. Výjimku tvoří ostrovy, které se sice nacházejí uprostřed oceánů. Navíc kvůli různorodému tvaru dna a pobřeží se dmutí často objevuje až s několikahodinovým szpožděním proti teoretickému modelu.
Amplituda dmutí je, jak bylo výše napsáno, nejnižší v místech uprostřed oceánů, naopak nejvyšší je typicky v úzkých dlouhých zálivech na pobřeží. Místem s nejvyšší amplitudou dmutí je Záliv Fundy v severní Americe, kde rozdíl mezi přílivem a odlivem dosahuje až 16 metrů[2]. V Evropě je největší rozpětí přílivu a odlivu poblíž pobřeží Francie v zátoce Mont-Saint-Michel, kde dosahuje až 15 metrů[3].
Mechanismus přílivu a odlivu[editovat | editovat zdroj]
K přílivu a odlivu dochází s dvojnásobkem frekvence, odpovídající průchodu Měsíce nad příslušným poledníkem, tj. každých 12 hodin 25 minut a 14 sekund. Interval mezi přílivem a odlivem na stejném místě je tedy 6 hodin, 12 minut a 37 sekund.
Isaac Newton laid the foundations for the mathematical explanation of tides in the Philosophiae Naturalis Principia Mathematica (1687). In 1740, the Académie Royale des Sciences in Paris offered a prize for the best theoretical essay on tides. Daniel Bernoulli, Antoine Cavalleri, Leonhard Euler, and Colin Maclaurin shared the prize. Maclaurin used Newton’s theory to show that a smooth sphere covered by a sufficiently deep ocean under the tidal force of a single deforming body is a prolate spheroid with major axis directed toward the deforming body. Maclaurin was the first to write about the Earth's rotational effects on motion. Euler realized that the horizontal component of the tidal force (more than the vertical) drives the tide.
In 1744 Jean le Rond d'Alembert studied tidal equations for the atmosphere which did not include rotation. The first major theoretical formulation for water tides was made by Pierre-Simon Laplace, who formulated a system of partial differential equations relating the horizontal flow to the surface height of the ocean. The Laplace tidal equations are still in use today. William Thomson, 1st Baron Kelvin, rewrote Laplace's equations in terms of vorticity which allowed for solutions describing tidally driven coastally trapped waves, which are known as Kelvin waves.[4]
Regarding the Earth–Moon system by itself (excluding the Sun for the moment) it is known that unless the spin axes of both partners are aligned and perpendicular to the orbital plane, oscillations are excited and these tidal deformations attribute somewhat to the tidal dissipation.[5] This lack of alignment is the case for the Earth–Moon system. Thus, besides the tidal bulges, opposite to each other and comparable in size, that are associated with the so called equilibrium tide,[6]additionally, a set of surface oscillations commonly known as the dynamical tide, characterized by a wide variety of harmonic frequencies, is established.[7][8][9]
Síly[editovat | editovat zdroj]
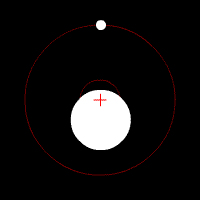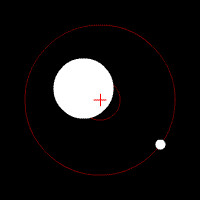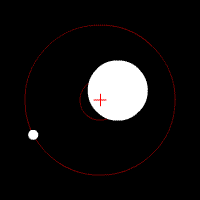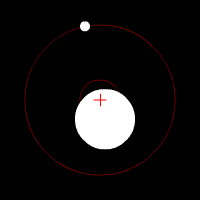
The tidal force produced by a massive object (Moon, hereafter) on a small particle located on or in an extensive body (Earth, hereafter) is the vector difference between the gravitational force exerted by the Moon on the particle, and the gravitational force that would be exerted on the particle if it were located at the center of mass of the Earth. Thus, the tidal force depends not on the strength of the gravitational field of the Moon, but on its gradient (which falls off approximately as the inverse cube of the distance to the originating gravitational body; see NASA).[10] The gravitational force exerted on the Earth by the Sun is on average 179 times stronger than that exerted on the Earth by the Moon, but because the Sun is on average 389 times farther from the Earth, the gradient of its field is weaker. The tidal force produced by the Sun is therefore only 46% as large as that produced by the Moon. (According to NASA the tidal force of the Moon is 2.21 times larger than that of the Sun. The effect of the other planets is much, much smaller, with the largest being Venus at 0.000113 times that of the Sun.)
Tidal forces can also be analyzed from the point of view of a reference frame that translates with the center of mass of the Earth. Consider the tide due to the Moon (the Sun is similar). First observe that the Earth and Moon rotate around a common orbital center of mass (called the barycenter), as determined by their relative masses. See Figure 6. The orbital center of mass is 3/4 of the way from the Earth's center to its surface. The second observation is that Figure 6 shows that the points on the Earth's surface farthest from the Moon rotate about the barycenter at a larger radius than those points closest to the Moon. Consequently, they experience a larger centrifugal force pointing outward, away from the barycenter. (Centrifugal force is proportional to radius). This outward force reduces the effective gravitational attraction of the Earth on the far side more than on the near side.[11] Besides the outward centrifugal force, however, each point of the Earth experiences the Moon's radially decreasing gravity differently; they are subject to the tidal forces of Figure 7, which dominate. Finally, most importantly, only the horizontal components of the tidal forces actually contribute tidal acceleration to the water particles since there is small resistance. The actual tidal force on a particle is only about a ten millionth of the force caused by the Earth's gravity.

The ocean's surface is closely approximated by an equipotential surface, (ignoring ocean currents) which is commonly referred to as the geoid. Since the gravitational force is equal to the gradient of the potential, there are no tangential forces on such a surface, and the ocean surface is thus in gravitational equilibrium. Now consider the effect of external, massive bodies such as the Moon and Sun. These bodies have strong gravitational fields that diminish with distance in space and which act to alter the shape of an equipotential surface on the Earth. Gravitational forces follow an inverse-square law (force is inversely proportional to the square of the distance), but tidal forces are inversely proportional to the cube of the distance. The ocean surface moves to adjust to changing tidal equipotential, tending to rise when the tidal potential is high, the part of the Earth nearest the Moon, and the farthest part. When the tidal equipotential changes, the ocean surface is no longer aligned with it, so that the apparent direction of the vertical shifts. The surface then experiences a down slope, in the direction that the equipotential has risen.
Amplituda a perioda[editovat | editovat zdroj]
The theoretical amplitude of oceanic tides caused by the Moon is about 54 cm at the highest point, which corresponds to the amplitude that would be reached if the ocean possessed a uniform depth, there were no landmasses, and the Earth were not rotating. The Sun similarly causes tides, of which the theoretical amplitude is about 25 cm (46% of that of the Moon) with a cycle time of 12 hours. At spring tide the two effects add to each other to a theoretical level of 79 cm, while at neap tide the theoretical level is reduced to 29 cm. Since the orbits of the Earth about the Sun, and the Moon about the Earth, are elliptical, the amplitudes of the tides change somewhat as a result of the varying Earth–Sun and Earth–Moon distances. This causes a variation in the tidal force and theoretical amplitude of about ±18% for the Moon and ±5% for the Sun. If both the Sun and Moon were at their closest positions and aligned at new moon, the theoretical amplitude would reach 93 cm.
Real amplitudes differ considerably, not only because of variations in ocean depth, and the obstacles to flow caused by the continents, but also because the natural period of wave propagation is of the same order of magnitude as the rotation period: about 30 hours. If there were no land masses, it would take about 30 hours for a long wavelength ocean surface wave to propagate along the equator halfway around the Earth (by comparison, the natural period of the Earth's lithosphere is about 57 minutes).
Dissipation[editovat | editovat zdroj]
The tidal oscillations of the Earth introduce dissipation, at an average rate of about 3.75 terawatt.[12] About 98% of this dissipation is by the tidal movement in the seas and oceans.[13] The dissipation arises as the basin-scale tidal flow drives smaller-scale flows which experience turbulent dissipation. This tidal drag gives rise to a torque on the Moon that results in the gradual transfer of angular momentum to its orbit, and a gradual increase in the Earth–Moon separation. As a result of the equal and opposite torque on the Earth, the rotational velocity of the Earth is correspondingly slowed. Thus, over geologic time, the Moon recedes from the Earth, at about 3.8 cm/year, and the length of the terrestrial day increases, meaning that there is about 1 fewer day per 100 million years.[14]
Observation and prediction[editovat | editovat zdroj]
History[editovat | editovat zdroj]
From ancient times, tides have been observed and discussed with increasing sophistication, first noting the daily recurrence, then its relationship to the Sun and Moon. Pytheas travelled to the British Isles and seems to be the first to have related spring tides to the phase of the Moon.
In the 2nd century BC, the Babylonian astronomer, Seleucus of Seleucia, correctly described the phenomenon of tides in order to support his heliocentric theory.[15] He correctly theorized that tides were caused by the Moon, although he believed that the interaction was mediated by the pneuma. He noted that the tides varied in time and strength in different parts of the world. According to Strabo (1.1.9), Seleucus was the first to state that the tides are due to the attraction of the Moon, and that the height of the tides depends on the Moon's position relative to the Sun.[16]
The Naturalis Historia of Pliny the Elder collates many observations of detail: the spring tides being a few days after (or before) new and full moon, and that the spring tides around the time of the equinoxes were the highest, though there were also many relationships now regarded as fanciful. In his Geography, Strabo described tides in the Persian Gulf having their greatest range when the Moon was furthest from the plane of the equator. All this despite the relatively feeble tides in the Mediterranean basin, though there are strong currents through the Strait of Messina and between Greece and the island of Euboea through the Euripus that puzzled Aristotle. In Europe around 730 AD, the Venerable Bede described how the rise of tide on one coast of the British Isles coincided with the fall on the other and described the progression in times of the same high water along the Northumbrian coast.
In the 9th century, the Arabian earth-scientist, Al-Kindi (Alkindus), wrote a treatise entitled Risala fi l-Illa al-Failali l-Madd wa l-Fazr (Treatise on the Efficient Cause of the Flow and Ebb), in which he presents an argument on tides which "depends on the changes which take place in bodies owing to the rise and fall of temperature."[17] He describes a clear and precise laboratory experiment in order to prove his argument.[18]
The first tide table in China was recorded in 1056 A.D, primarily for the benefit of visitors wishing to see the famous tidal bore in the Qiantang River. The first known tide table is thought to be that of John, Abbott of Wallingford (d. 1213), based on high water occurring 48 minutes later each day, and three hours later upriver at London than at the mouth of the Thames.
William Thomson (Lord Kelvin) led the first systematic harmonic analysis of tidal records starting in 1867. The main result was the building of a tide-predicting machine using a system of pulleys to add together six harmonic functions of time. It was "programmed" by resetting gears and chains to adjust phasing and amplitudes. Similar machines were used until the 1960s.
The first known sea-level record of an entire spring–neap cycle was made in 1831 on the Navy Dock in the Thames Estuary, and many large ports had automatic tide gage stations by 1850.
William Whewell first mapped co-tidal lines ending with a nearly global chart in 1836. In order to make these maps consistent, he hypothesized the existence of amphidromes where co-tidal lines meet in the mid-ocean. These points of no tide were confirmed by measurement in 1840 by Captain Hewett, RN, from careful soundings in the North Sea.[4]
Timing[editovat | editovat zdroj]

In most places there is a delay between the phases of the Moon and the effect on the tide. Springs and neaps in the North Sea, for example, are two days behind the new/full Moon and first/third quarter. This is called the age of the tide.[19]
The exact time and height of the tide at a particular coastal point is also greatly influenced by the local bathymetry. There are some extreme cases: the Bay of Fundy, on the east coast of Canada, features the largest well-documented tidal ranges in the world, 16 meters (53 ft), because of the shape of the bay.[20] Ungava Bay in northern Quebec, is believed by some experts to have higher tidal ranges than the Bay of Fundy, but it is free of pack ice for only about four months every year, whereas the Bay of Fundy rarely freezes.
Southampton in the United Kingdom has a double high water caused by the interaction between the different tidal harmonics within the region. This is contrary to the popular belief that the flow of water around the Isle of Wight creates two high waters. The Isle of Wight is important, however, since it is responsible for the 'Young Flood Stand', which describes the pause of the incoming tide about three hours after low water.[21]
Because the oscillation modes of the Mediterranean Sea and the Baltic Sea do not coincide with any significant astronomical forcing period, the largest tides are close to their narrow connections with the Atlantic Ocean. Extremely small tides also occur for the same reason in the Gulf of Mexico and Sea of Japan. On the southern coast of Australia, because the coast is mainly straight (partly because of the tiny quantities of runoff flowing from rivers), tidal ranges are equally small.
Analysis[editovat | editovat zdroj]
It was Isaac Newton's universal theory of gravitation that first enabled an explanation of why there were two tides a day, not one, and, via calculation of the forces, offered hope of detailed understanding. Although it may seem that tides could be predicted via a sufficiently detailed knowledge of the astronomical forcing terms, the actual tide at a given location is determined by the response of the oceans to the astronomical forces accumulated over a period of many days. To calculate this response requires a detailed knowledge of the shape of all the ocean basins — their bathymetry and coastline shape.
Instead of a direct calculation, the procedure for analysing tides is pragmatic: At each place of interest, the tide heights are measured for at least a lunar cycle. The tide heights are compared to the known frequencies of the astronomical tide-raising forces. The behaviour of the tide heights is expected to follow the behaviour of the tide force, with the amplitude and delays of those responses remaining constant. Because astronomical frequencies and phases can be calculated with certainty, the tide height at other times can be predicted once the response to the astronomical states has been found.
The main patterns in the tides are
- the twice-daily combined lunar and solar tide, caused by the rotation of the Earth,
- the difference between the first and second tide of a day, due to the Moon or Sun being north or south of the equator,
- the spring-neap cycle in amplitude (related to the relative positions of the Moon and Sun), and
- the adjustment of spring tide heights due to the varying distances to the Moon and Sun.
The Highest Astronomical Tide is the perigean spring tide when both the Sun and the Moon are closest to the Earth.
When confronted by a periodically varying function, the standard approach is to employ Fourier series, a form of orthogonal analysis that uses sinusoidal functions as a basis set, having frequencies that are zero, one, two, three, etc. times the frequency of a particular fundamental cycle. These multiples are called harmonics of the fundamental frequency, and the process is termed harmonic analysis. If the basis set of sinusoidal functions are well-suited to the behaviour being modelled, relatively few harmonic terms need to be carried in the analysis. Fortunately orbital paths are very nearly circular, so sinusoidal variations are suitable for tides.
For the analysis of tide heights, the Fourier series approach is best made more elaborate. While the theorem remains true and the tidal height could be analysed in terms of a single frequency and its harmonics, a large number of significant terms would be required. A much more compact decomposition for the tides involves a combination of sinusoids having more than one fundamental frequency. Specifically, the incommensurable periods of one revolution of the Earth (equivalently, of the Sun around the Earth), and one orbit of the Moon about the Earth are used (for simplicity in phrasing, this discussion is entirely geocentric, but is informed by the heliocentric model).
To represent both the lunar and solar influences using one frequency would require many harmonic terms, but allowing two incommensurable frequencies requires only a few terms. That is, the sum of two sinusoids, one at the Sun's frequency and the second at the Moon's frequency, requires those two terms only, but their representation as a Fourier series having only one fundamental frequency and its (integer) multiples would require many terms. For tides then, although the process is still termed harmonic analysis, it is not limited to harmonics of a single frequency. To demonstrate this [22] offers a tidal height pattern converted into an .mp3 sound file, and the rich sound is quite different from a pure tone. In other words, the harmonies are multiples of many fundamental frequencies, not just of the one fundamental frequency of the simpler Fourier series approach.
The study of tide height by harmonic analysis was begun by Laplace, William Thomson (Lord Kelvin), and George Darwin. Their work was extended by A.T. Doodson who introduced the Doodson Number notation to organise the hundreds of terms that result. This approach has been the international standard ever since, and the complications arise as follows: the tide-raising force is notionally given by sums of several terms. Each term is of the form
- A·cos(w·t + p)
where A is the amplitude, w is the angular frequency usually given in degrees per hour corresponding to t measured in hours, and p is the phase offset with regard to the astronomical state at time t = 0 . There is one term for the Moon and a second term for the Sun. If the orbits were circular, that would be the end of the matter, but of course they are not. Accordingly, the value of A is not a constant but also varying with time, slightly, about some average figure. Replace it then by A(t) , but what functional form? It turns out that another sinusoid gives an excellent approximation for the changing amplitude, similar to the cycles and epicycles of Ptolemaic theory. Accordingly,
- A(t) = A·(1 + Aa·cos(wa·t + pa)) ,
which is to say an average value A with a sinusoidal variation about it of magnitude Aa , with frequency wa and phase pa . Thus the simple term is now a compound term, the product of two cosine factors:
- A·[1 + Aa·cos(wa + pa)]·cos(w·t + p)
Now, given that for any x and y
- cos(x)·cos(y) = ½·cos( x + y ) + ½·cos( x – y ) ,
it is clear that a compound term involving the product of two cosine terms each with their own frequency is the same as three simple cosine terms that are to be added, at the original frequency and also at the sum and difference of the two frequencies of the product term. (Three, not two terms, since the whole expression is (1 + cos(x))·cos(y) .) Consider further that the tidal force on a location depends also on whether the Moon (or the Sun) is above or below the plane of the equator, and that these attributes have their own periods also incommensurable with a day and a month, and it is clear that many combinations result. With a careful choice of the basic astronomical frequencies, the Doodson Number annotates the particular additions and differences of them to form the frequency of each simple cosine term.
Remember that astronomical tides do not include the effect of weather, and changes to local conditions (sandbank movement, dredging harbour mouths, etc.) away from those prevailing at the time of measurement can affect the timing and magnitude of the actual tide. Organisations quoting a "highest astronomical tide" for some location can exaggerate the figure as a safety factor against uncertainties of analysis, extrapolation from the nearest point of measurement, changes since the time of observation, possible ground subsidence, etc., to protect the organisation against blame should an engineering work be overtopped. If the size of a "weather surge" is assessed by subtracting the astronomical tide from the observed tide at the time, care is needed.
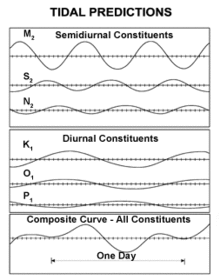
Careful Fourier data analysis over a nineteen-year period (the National Tidal Datum Epoch in the U.S.) uses frequencies called the tidal harmonic constituents. Nineteen years is preferred because the relative positions of the Earth, Moon and Sun repeat almost exactly in the Metonic cycle of 18.6 years. This analysis can be done using only the knowledge of the period of forcing, but without detailed understanding of the mathematical derivation, which means that useful tidal tables have been constructed for centuries.[23] The resulting amplitudes and phases can then be used to predict the expected tides. These are usually dominated by the constituents near 12 hours (the semidiurnal constituents), but there are major constituents near 24 hours (diurnal) as well. Longer term constituents are 14 day or fortnightly, monthly, and semiannual. Most of the coastline is dominated by semidiurnal tides, but some areas such as the South China Sea and the Gulf of Mexico are primarily diurnal. In the semidiurnal areas, the primary constituents M2 (lunar) and S2 (solar) periods differ slightly, so that the relative phases, and thus the amplitude of the combined tide, change fortnightly (14 day period).[24]
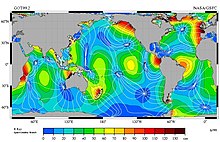
In the M2 plot above each cotidal line differs by one hour from its neighbors, and the thicker lines show tides in phase with equilibrium at Greenwich. The lines rotate around the amphidromic points counterclockwise in the northern hemisphere so that from Baja California to Alaska and from France to Ireland the M2 tide propagates northward. In the southern hemisphere this direction is clockwise. On the other hand M2 tide propagates counterclockwise around New Zealand, but this because the islands act as a dam and permit the tides to have different heights on opposite sides of the islands. (But the tides do propagate northward on the east side and southward on the west coast, as predicted by theory.)
The exception is the Cook Strait where the tidal currents periodically link high to low water. This is because cotidal lines 180° around the amphidromes are in opposite phase, for example high water across from low water. Each tidal constituent has a different pattern of amplitudes, phases, and amphidromic points, so the M2 patterns cannot be used for other tide components.
Current[editovat | editovat zdroj]
The flow pattern caused by tidal influence is much more difficult to analyse, and also, data is much more difficult to collect. A tidal height is a simple number which applies to a wide region simultaneously — often as far as the eye can see. A flow has both a magnitude and a direction, which both can vary substantially over just a short distance due to local bathymetry, and also vary with depth below the water surface. Also, although the centre of a channel is the most useful measuring site, mariners will not accept a current measuring installation obstructing navigation, so a flexible approach is required. A flow proceeding up a curved channel is the same flow, even though its direction varies continuously along the channel. But contrary even to the obvious expectation, flood and ebb flows are often not in opposite directions. The direction of a flow is determined by the shape of the channel it is coming from, not the shape where it will shortly be. Likewise, eddies can form in one direction but not the other.
Nevertheless, analysis of currents proceeds on the same basis as tides: At a given location in the simple case, the great majority of the flood flow will be in one direction, and the ebb flow in another (not necessarily opposite) direction. The velocities measured along the flood direction are taken as positive, and along the ebb direction as negative, and analysis proceeds as if these were tide height figures.
In more complex situations, the flow will not be dominated by the main ebb and flow directions, with the flow direction and magnitude tracing out an ellipse over a tidal cycle (on a polar plot) instead of along the two lines of ebb and flow direction. In this case, analysis might proceed along two pairs of directions, the primary flow directions and the secondary directions at right angles. Alternatively, the tidal flows can be treated as complex numbers, as each value has both a magnitude and a direction.
As with tide height predictions, tide flow predictions based only on astronomical factors do not take account of weather conditions, which can completely change the situation.
The tidal flow through Cook Strait between the two main islands of New Zealand is particularly interesting, as on each side of the strait the tide is almost exactly out of phase so that high water on one side meets low water on the other. Strong currents result, with almost zero tidal height change in the centre of the strait. Yet, although the tidal surge should flow in one direction for six hours and then the reverse direction for six hours, a particular surge might last eight or ten hours with the reverse surge enfeebled. In especially boisterous weather conditions, the reverse surge might be entirely overcome so that the flow remains in the same direction through three surge periods and longer. A further complication for Cook Strait's pattern of current flow is that the tides at the north end have the ordinary two cycles of spring-neap tides in a month (as found along the west side of the country), but the south end's tidal pattern has only one cycle of spring-neap tides a month, as found on the east side of the country. Tidal currents are much more complex than tidal heights!
Power generation[editovat | editovat zdroj]
- Hlavní článek: Tidal power
{{unbalanced}}
Power can be extracted by two means: inserting a water turbine into a tidal current, or building impoundment ponds so as to release or admit water through a turbine. In the first case, the generation is entirely determined by the timing and magnitude of the tidal currents, and the best currents may be unavailable because the turbines would obstruct navigation. In the second, the impoundment dams are expensive to construct, the natural water cycles are completely disrupted, as is navigation, but with multiple impoundment ponds power can be generated at chosen times. So far, there are few systems for tidal power generation (most famously, La Rance by Saint Malo, France) and many difficulties. Aside from environmental issues, simply withstanding sea-water corrosion and fouling by biological growths poses engineering challenges.
Proponents of tidal power systems point out that, unlike wind power systems, the generation pattern can be predicted years ahead. However, weather effects are still problematic. Another assertion is that some generation is possible for most of the tidal cycle. This may be true in principle since the time of still water is short, but in practice turbines lose efficiency at partial operating powers. Since the power available from a flow is proportional to the cube of the flow speed, the times during which high power generation is possible turn out to be rather brief. An obvious fallback then is to have several tidal power generation stations, at locations where the tide phase is different enough so that low power from one station is filled in by high power from another. Again, New Zealand has particularly interesting opportunities. Because the tidal pattern is such that a state of high water orbits the country once per cycle, there is always somewhere around the coast where the tide is at its peak, and somewhere else where it is at its lowest, so that via the electricity transmission network, there could always be supply from tidal generation somewhere. The most convenient situation is presented with Auckland city, which is between Manukau harbour and Waitemata harbour so that both power stations would be close to the load.
But, because the power available varies with the cube of the flow, even with the optimum phase difference of three hours between two stations, there are still significant amounts of time when neither tidal flow is rapid enough for significant generation, and worse, during the time of neap tides, the flow is weak all of the day, and there is no getting around this via multiple stations, because the neap tides apply to the whole Earth at once. The most feeble neap tides would be when the Sun's influence is maximum whilst the Moon's is weakest, and as far as the Sun is concerned, it is closest to the Earth during the time of the southern hemisphere's summer, which is when electricity demand is the least there, a small bonus.
As a result, interest must fall on the Kaipara harbour which not only is large, but also is two-lobed in shape, and thus almost pre-designed for a tidal impoundment scheme where one lobe could be filled by high water and the other emptied by a low water, and then via a canal from one to the other generation would be possible at a time of choice.
There is scant likelihood of any such scheme proceeding because of the disruption to natural conditions.
[editovat | editovat zdroj]
Tidal flows are of importance in navigation, and significant errors in position will occur if they are not taken into account. Tidal heights are also important; for example many rivers and harbours have a shallow "bar" at the entrance which will prevent boats with significant draft from entering at certain states of the tide.
The timings and velocities of tidal flow can be found by looking at a tidal chart or tidal stream atlas for the area of interest. Tidal charts come in sets, with each diagram of the set covering a single hour between one high water and another (they ignore the extra 24 minutes) and give the average tidal flow for that one hour. An arrow on the tidal chart indicates the direction and the average flow speed (usually in knots) for spring and neap tides. If a tidal chart is not available, most nautical charts have "tidal diamonds" which relate specific points on the chart to a table of data giving direction and speed of tidal flow.
Standard procedure to counteract the effects of tides on navigation is to (1) calculate a "dead reckoning" position (or DR) from distance and direction of travel, (2) mark this on the chart (with a vertical cross like a plus sign) and (3) draw a line from the DR in the direction of the tide. The distance the tide will have moved the boat along this line is computed by the tidal speed, and this gives an "estimated position" or EP (traditionally marked with a dot in a triangle).

Nautical charts display the "charted depth" of the water at specific locations with "soundings" and the use of bathymetric contour lines to depict the shape of the submerged surface. These depths are relative to a "chart datum", which is typically the level of water at the lowest possible astronomical tide (tides may be lower or higher for meteorological reasons) and are therefore the minimum water depth possible during the tidal cycle. "Drying heights" may also be shown on the chart, which are the heights of the exposed seabed at the lowest astronomical tide.
Heights and times of low and high water on each day are published in tide tables. The actual depth of water at the given points at high or low water can easily be calculated by adding the charted depth to the published height of the tide. The water depth for times other than high or low water can be derived from tidal curves published for major ports. If an accurate curve is not available, the rule of twelfths can be used. This approximation works on the basis that the increase in depth in the six hours between low and high water will follow this simple rule: first hour - 1/12, second - 2/12, third - 3/12, fourth - 3/12, fifth - 2/12, sixth - 1/12.
Biological aspects[editovat | editovat zdroj]
Intertidal ecology[editovat | editovat zdroj]

- Hlavní článek: Intertidal ecology
Intertidal ecology is the study of intertidal ecosystems, where organisms live between the low and high water lines. At low water, the intertidal is exposed (or ‘emersed’) whereas at high water, the intertidal is underwater (or ‘immersed’). Intertidal ecologists therefore study the interactions between intertidal organisms and their environment, as well as between different species of intertidal organisms within a particular intertidal community. The most important environmental and species interactions may vary based on the type of intertidal community being studied, the broadest of classifications being based on substrates - rocky shore and soft bottom communities.
Organisms living in this zone have a highly variable and often hostile environment, and have evolved various adaptations to cope with and even exploit these conditions. One easily visible feature of intertidal communities is vertical zonation, where the community is divided into distinct vertical bands of specific species going up the shore. A species' ability to cope with desiccation determines their upper limits, while competition with other species sets their lower limits.
Intertidal regions are utilized by humans for food and recreation, but anthropogenic actions also have major impacts, with overexploitation, invasive species and climate change being among the problems faced by intertidal communities. In some places Marine Protected Areas have been established to protect these areas and aid in scientific research.
Biological rhythms[editovat | editovat zdroj]
Intertidal organisms are greatly affected by the approximately fortnightly cycle of the tides, and hence their biological rhythms tend to occur in rough multiples of this period. This is seen not only in the intertidal organisms however, but also in many other terrestrial animals, such as the vertebrates. Examples include gestation and the hatching of eggs. In humans, for example, the menstrual cycle lasts roughly a month, an even multiple of the period of the tidal cycle. This may be evidence of the common descent of all animals from a marine ancestor.[25]
Other tides[editovat | editovat zdroj]
In addition to oceanic tides, there are atmospheric tides as well as earth tides. All of these are continuum mechanical phenomena, the first two being fluids and the third solid (with various modifications).
Atmospheric tides are negligible from ground level and aviation altitudes, drowned by the much more important effects of weather. Atmospheric tides are both gravitational and thermal in origin and are the dominant dynamics from about 80 km to 120 km where the molecular density becomes too small to behave as a fluid.
Earth tides or terrestrial tides affect the entire rocky mass of the Earth. The Earth's crust shifts (up/down, east/west, north/south) in response to the Moon's and Sun's gravitation, ocean tides, and atmospheric loading. While negligible for most human activities, the semidiurnal amplitude of terrestrial tides can reach about 55 cm at the equator (15 cm is due to the Sun) which is important in GPS calibration and VLBI measurements. Also to make precise astronomical angular measurements requires knowledge of the Earth's rate of rotation and nutation, both of which are influenced by earth tides. The semi-diurnal M2 Earth tides are nearly in phase with the Moon with tidal lag of about two hours.[26] Terrestrial tides also need to be taken in account in the case of some particle physics experiments.[27] For instance, at the CERN or SLAC, the very large particle accelerators were designed while taking terrestrial tides into account for proper operation. Among the effects that need to be taken into account are circumference deformation for circular accelerators and particle beam energy.[28] Since tidal forces generate currents of conducting fluids within the interior of the Earth, they affect in turn the Earth's magnetic field itself.
When oscillating tidal currents in the stratified ocean flow over uneven bottom topography, they generate internal waves with tidal frequencies. Such waves are called internal tides.
The galactic tide is the tidal force exerted by galaxies on stars within them and satellite galaxies orbiting them. The effects of the galactic tide on the Solar System's Oort cloud are believed to be the cause of 90 percent of all observed long-period comets.[29]
Misapplications[editovat | editovat zdroj]
Tsunamis, the large waves that occur after earthquakes, are sometimes called tidal waves, but this name is given by their resemblance to the tide, rather than any actual link to the tide. Other phenomena unrelated to tides but using the word tide are rip tide, storm tide, hurricane tide, and black or red tides.
Reference[editovat | editovat zdroj]
- ↑ Slapové jevy: příliv a odliv [online]. Strany potápěčské [cit. 2008-07-28]. Dostupné online.
- ↑ BAYOFFUNDY.COM. Highest Tides in the World [online]. [cit. 2008-12-26]. Dostupné online. (anglicky)
- ↑ OT-MONTSAINTMICHEL.COM. Times of the tides [online]. [cit. 2008-12-26]. Dostupné online. (anglicky)
- ↑ a b "Historical Development and Use of Thousand-Year-Old Tide-Prediction Tables," Yang Zuosheng, K. O. Emery, Xui Yui, Limnology and Oceanography, Vol. 34, No. 5 (Jul., 1989), pp. 953-957. Tides: A Scientific History, David E. Cartwright, Cambridge University Press, Cambridge, UK, 1999. reviewed in "Understanding Tides—From Ancient Beliefs to Present-day Solutions to the Laplace Equations," James Case, SIAM News, Volume 33, Number 2 March 2000.
- ↑ The dissipation by internal fluctuating deformations of the Earth due to the tidal force of the Moon is small as compared with the tidal dissipation in the Earth's oceans and seas, which attribute for 98% of the reduction of the Earth's rotational energy. See:Ray, R. D. Detection of tidal dissipation in the solid Earth by satellite tracking and altimetry. Nature. 1996, roč. 381, s. 595. DOI 10.1038/381595a0.
- ↑ John D. Boon. Secrets Of The Tide: Tide And Tidal Current Analysis And Applications, Storm Surges And Sea Level Trends. [s.l.]: Hollywood Publishing, 2004. Dostupné online. ISBN 1904275176. S. Chapter 2 pp. 13-end.
- ↑ Toledano et al. (2008) Tides in asynchronous binary systems
- ↑ Horace Lamb. Hydrodynamics. 4th Edition. vyd. [s.l.]: Cambridge University Press, 1916. Dostupné online. S. p. 339.
- ↑ Rollin A Harris. The Encyclopedia Americana: A Library of Universal Knowledge. [s.l.]: Encyclopedia Americana, 1918. Dostupné online. S. Article on Tides, pp. 613-614.
- ↑ Two points on either side of the Earth sample the imposed gravity at two nearby points, effectively providing a finite difference of the gravitational force that varies as the inverse square of the distance. The derivative of 1/r2, with r = distance to originating body, varies as the inverse cube.
- ↑ Compare this to passengers on a turning bus. The bus's overall motion follows the center of mass, but passengers sitting in different parts of the bus experience different forces, and so may shift within the bus. The rigid body of the bus redistributes the road traction forces through its frame and seats to the passengers, who experience the sideways traction of the seat. There is relatively small difference between the way the entire bus responds to the turn compared to individual passengers, and their movement relative to the bus is much smaller than the turning motion of the bus. Like the bus, the Earth does deform some, but the oceans still are subject to a residual forcing.
- ↑ Munk, W. Abyssal recipes II: energetics of tidal and wind mixing. Deep Sea Research Part I Oceanographic Research Papers. 1998, roč. 45, s. 1977. DOI 10.1016/S0967-0637(98)00070-3.
- ↑ Ray, R. D. Detection of tidal dissipation in the solid Earth by satellite tracking and altimetry. Nature. 1996, roč. 381, s. 595. DOI 10.1038/381595a0.
- ↑ Lecture 2: The Role of Tidal Dissipation and the Laplace Tidal Equations by Myrl Hendershott. GFD Proceedings Volume, 2004, WHOI Notes by Yaron Toledo and Marshall Ward.
- ↑ Lucio Russo, Flussi e riflussi, Feltrinelli, Milano, 2003, ISBN 88-07-10349-4.
- ↑ Bartel Leendert van der Waerden (1987). "The Heliocentric System in Greek, Persian and Hindu Astronomy", Annals of the New York Academy of Sciences 500 (1), 525–545 [527].
- ↑ Al-Kindi, FSTC
- ↑ Plinio Prioreschi, "Al-Kindi, A Precursor Of The Scientific Revolution", Journal of the International Society for the History of Islamic Medicine, 2002 (2): 17-19 [17]
- ↑ Glossary of Meteorology American Meteorological Society.
- ↑ http://www.waterlevels.gc.ca/english/FrequentlyAskedQuestions.shtml#importantes, accessed June 23, 2007
- ↑ http://www.bristolnomads.org.uk/stuff/double_tides.htm, accessed April 24, 2008
- ↑ Tides Home Page
- ↑ Tide and Current Glossary, Center for Operational Oceanographic Products and Services, National Ocean Service, National Oceanic and Atmospheric Administration, Silver Spring, MD, January 2000.
- ↑ Harmonic Constituents,NOAA.
- ↑ Darwin, Charles (1871). The Descent of Man, and Selection in Relation to Sex. John Murray: London.
- ↑ Earth tide calculator
- ↑ Linac, Stanford online.
- ↑ "Effects of Tidal Forces on the Beam Energy in LEP", PAC 1993, IEEE. "Long term variation of the circumference of the spring-8 storage ring", Proceedings of EPAC 2000, Vienna, Austria.
- ↑ Periodic variation of Oort Cloud flux and cometary impacts on the Earth and Jupiter. Monthly Notices of the Royal Astronomical Society. 2001, roč. 327, s. 1367–1376. Dostupné online. DOI 10.1046/j.1365-8711.2001.04854.x.
Externí odkazy[editovat | editovat zdroj]
- Slapové jevy: příliv a odliv na Stranách potápěčských
- O. Toledano et al. (2008): Tides in asynchronous binary systems
- Earth, Atmospheric, and Planetary Sciences MIT Open Courseware; Ch 8 §3
- Eugene I. Butikov: A dynamical picture of the ocean tides
- Planetary alignment and the tides (NASA)
- Oceanography: tides by J. Floor Anthoni (2000).
- Myths about Gravity and Tides by Mikolaj Sawicki (2005).
- Tidal Misconceptions by Donald E. Simanek.
- Our Restless Tides: NOAA's practical & short introduction to tides.
- Tides and centrifugal force: Why the centrifugal force does not explain the tide's opposite lobe (with nice animations).
Tide predictions[editovat | editovat zdroj]
- National Oceanic and Atmospheric Administration (NOAA)
- WWW Tide and Current Predictor
- XTide Tide Prediction Server
- Tides: Why They Happen -- Beaufort County Library
- Australian Tide Times
- Department of Oceanography, Texas A&M University
- UK, South Atlantic, British Overseas Territories and Gibraltar tide times from the UK National Tidal and Sea Level Facility
- UK Admiralty Easytide
- History of tide prediction
V tomto článku byl použit překlad textu z článku Tide na anglické Wikipedii.
</ref>
-->
![]() Obrázky, zvuky či videa k tématu Kubajzz/odkladiste na Wikimedia Commons
Obrázky, zvuky či videa k tématu Kubajzz/odkladiste na Wikimedia Commons
