Strahlerovo číslo

Schéma znázorňující Strahlerovu klasifikaci vodních toků

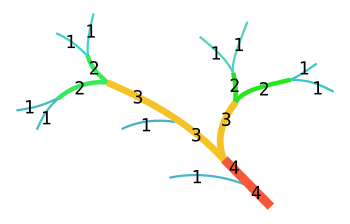
Strahlerovo číslo (někdy také Horton–Strahlerovo číslo) se v matematice používá k označení jednotlivých větví ve stromových digramech.

Poprvé čísla použili Robert E. Horton a Arthur Newell Strahler pro označení vodních toků v hydrologii. Podle Strahlerovy klasifikace vodních toků jsou přítoky hierarchicky číslovany podle velikosti. Metoda se také využívá při analýze L-systémů a hierarchicky uspořádaných biologických struktur, jako jsou dýchací a oběhové soustavy živočichů, při alokaci registrů pro kompilaci vysokoúrovňových programovacích jazyků a při analýze sociálních sítí. Alternativní systémy klasifikace vodních toků vyvinuli R. L. Shreve a J. H. Hodgkinson a kol. J. S. Smart předložil statistické srovnání Strahlerova a Shreveho systému, spolu s analýzou délek toků a internetových odkazů.

Definice

Všechny stromové diagramy jsou v tomto kontextu orientované grafy větvené od kořene k listům. Stupeň vrcholu (uzlu) v diagramu odkazuje na počet jeho dceřiných větví. Strahlerovo číslo je uzlům v grafu přiřazeno ve vzestupném pořadí dle následujícího klíče:

• Pokud je uzlem list (nemá žádné dceřiné větve), je jeho Strahlerovo číslo rovno jedné;
• pokud má uzel jednu větev se Strahlerovým číslem i a všechny ostatní větve mají Strahlerovo číslo menší než i, pak Strahlerovo číslo uzlu je i;
• pokud má uzel dvě nebo více větve se Strahlerovým číslem i a žádnou větev s vyšším číslem, pak Strahlerovo číslo uzlu je i+1.

Strahlerovo číslo stromového diagramu je číslo jeho kořenového uzlu.

Algoritmicky se čísla přiřazují metodou prohledávání do hloubky a následným procházením stromu. Stejná čísla mohou být také generována pomocí procesu prořezávání, během kterého dochází v několika fázích k zjednodušení stromu. V každé z fází jsou odstraněny všechny listové uzly a větve všech jednostupňových uzlů vedoucích k listům. Strahlerovo číslo uzlu je pořadí fáze, kterou by během tohoto procesu došlo k jeho odstranění. Číslo celého diagramu je počet fází potřebných k odstranění všech jeho uzlů. Strahlerovo číslo stromového diagramu je odpovídajícím způsobem možné definovat jako výšku největšího úplného binárního stromu, který může být homeomorficky vložen do daného stromu. Strahlerovo číslo uzlu ve stromovém diagramu obdobně odpovídá výšce největšího úplného binárního stromu, který lze vložit pod tento uzel.

Každý uzel se Stráhlerovým číslem i se musí skládat alespoň ze dvou uzlů s číslem i-1, čtyř uzlů s číslem i-2 atd., a alespoň 2ⁱ⁻¹ listů. Nejvyšší hodnota Strahlerova čísla pro stromový diagram s n uzly je proto log₂ n + 1. Pokud však diagram nevytvoří úplný binární strom, bude číslo nižší. U náhodně vybraného binárního stromu s n uzly se předpokládaná hodnota indexu kořenu nejpravděpodobněji blíží log₄n.

Aplikace

Říční sítě

V hydrologii se Strahlerovo číslo používá ke klasifikaci vodních toků. Každý tok v povodí je vnímán jako uzel stromového diagramu. Soutokem dvou toků prvního řádu vzniká tok druhého řádu. Dva toky druhého řádu tvoří po soutoku tok třetího řádu atd. Po soutoku toku vyššího s tokem nižšího řádu se řád hlavního (vyššího) toku nemění. Pokud se tedy do toku druhého řádu vlévá tok prvního řádu, je tok nadále označován je tok druhého řádu. Ke změně řádu dochází teprve po soutoku dvou toků druhého řádu. V hydrologii musí být stejně jako v případě stromových diagramů tok i-tého řádu napájen alespoň 2ⁱ⁻¹ různými přítoky prvního řádu. R. L. Shreve vyslovil hypotézu, podle které lze Horton–Strahlerovu klasifikaci uplatnit na všechny toky na Zemi. Pozdějším potvrzením hypotézy bylo také dokázáno, že neexistuje vysvětlení pro vznik systémů povodí a skladbu vodních toků v nich.

Hydrologie se zabývá stálými a občasnými vodními toky. Občasné vodní toky (také označované jako periodické) jsou takové, v jejichž přirozeném vodním režimu se vyskytuje období, ve kterém korytem neprotéká voda a tok není napájen podzemní vodou. Řád vodního toku může dosahovat hodnot od 1 (pro toky, které nemají přítoky) do 12 (ústí nejdelší a nejvodnatější řeky světa Amazonky). Největší řeky v České republice jsou sedmého až devátého řádu. Až 80 % všech světových řek spadá do skupin řek prvního až třetího řádu.

Stupeň rozvětvení říční sítě udává bifurkační poměr povodí. Pokud je jeho hodnota nízká, znamená to, že je voda koncentrována v jednom či několika málo korytech. V takovýchto povodích nastávají povodně s vyšší pravděpodobností než v povodích s vyšším bifurkačním poměrem, ve kterých je voda rovnoměrně rozložena do více koryt. Bifurkační poměr může také ukázat náchylnost k povodním v rámci jednoho povodí.

Jiné klasifikační systémy

Strahlerova klasifikace může být využita ve statistické analýze jakéhokoliv hierarchického systému:

• Arenas a kol. (2004) popisují aplikaci Horton–Strahlerova čísla při analýze sociálních sítí;
• Ehrenfeucht, Rozenberg & Vermeir (1981) použili variantu Strahlerova číslování, kterou nazvali stromová řada (listům je místo hodnoty jedna přiřazena nula), pro analýzu L-systémů;
• Strahlerovo číslování je také používáno v biologii, například pro označení větvení stromů či dýchací a oběhové soustavy zvířat.

Alokace registrů

Minimální počet registrů procesoru nutných k vyhodnocení binárního stromu při překladu vyššího programovacího jazyka do jazyka symbolických adres, je roven Strahlerovu číslu daného stromu. V tomto kontextu je Strahlerovo číslo nazýváno také číslo registru.

V některých případech binární strom vyžaduje více registrů, než je k dispozici. K jeho překladu do sledu příkazů pak může být použit Sethi–Ullmanův algoritmus, který maximálně využívá registry a minimalizuje využívání hlavní paměti a celkový počet příkazů ve finálním kódu.

Související parametry

Bifurkační poměr

S použitím Strahlerova čísla pro označení větví ve stromovém diagramu souvisí bifurkační poměr, který udává vyváženost diagramu. Pro každý řád i v hierarchii diagramu lze i-tý bifurkační poměr určit dle vzorce:

${\frac {n_{i}}{n_{i+1}}}$,

kde n_i označuje počet uzlů i-tého řádu.

V hydrologii poměr udává počet toků určitého řádu ($n_{i}$) ku počtu toků o řád vyšší ($n_{i+1}$).

Bifurkační poměr celého diagramu lze určit jako průměr bifurkačních poměrů jednotlivých řádů. Bifurkační poměr úplného binárního stromu je roven dvěma, u ostatních stromů je poměr menší. Bifurkační poměr je veličina bez jednotky.

Šířka cesty

Šířku cesty libovolného neorientovaného grafu G můžeme definovat jako nejmenší existující číslo w, pro které platí: neorientovaný podgraf G je podgrafem intervalového grafu H, jehož maximální klika má w+1 vrcholů.

Stromový diagram můžeme považovat za neorientovaný graf, pokud nebereme v potaz jeho kořeny a orientaci. Šířka cesty stromových diagramů se liší od jejich Strahlerova čísla, úzce s ním však souvisí. Pro šířku cesty w a Strahlerovo číslo s stromového diagramu platí nerovnost:

w ≤ s ≤ 2w + 2.

Na rozdíl od Strahlerova čísla se šířka cesty vztahuje i na cyklické grafy. Nelze ji však definovat pro jednotlivé uzly grafu, ale pouze pro graf jako celek.

Související články

• binární strom
• říční systém
• strom (graf)

Reference

V tomto článku byl použit překlad textu z článku Strahler number na anglické Wikipedii.

Literatura

• ARENAS, A.; DANON, L.; DÍAZ-GUILERA, A.; GLEISER, P. M.; GUIMERÁ, R. Community analysis in social networks. European Physical Journal B. 2004, s. 373–380. DOI 10.1140/epjb/e2004-00130-1. Bibcode 2004EPJB...38..373A. arXiv cond-mat/0312040. .
• BORCHERT, Rolf; SLADE, Norman A. Bifurcation ratios and the adaptive geometry of trees. Botanical Gazette. 1981, s. 394–401. DOI 10.1086/337238. JSTOR 2474363. .
• DEVROYE, Luc; KRUSZEWSKI, Paul. A note on the Horton–Strahler number for random trees. Information Processing Letters. 1995, s. 95–99. DOI 10.1016/0020-0190(95)00114-R. .
• DEVROYE, L.; KRUSZEWSKI, P. On the Horton–Strahler number for random tries. RAIRO Informatique Théorique et Applications. 1996, s. 443–456. Dostupné online. 
• EHRENFEUCHT, A.; ROZENBERG, G.; VERMEIR, D. On ETOL systems with finite tree-rank. SIAM Journal on Computing. 1981, s. 40–58. DOI 10.1137/0210004. .
• ERSHOV, A. P. On programming of arithmetic operations. Communications of the ACM. 1958, s. 3–6. DOI 10.1145/368892.368907. .
• FLAJOLET, P.; RAOULT, J. C.; VUILLEMIN, J. The number of registers required for evaluating arithmetic expressions. Theoretical Computer Science. 1979, s. 99–125. DOI 10.1016/0304-3975(79)90009-4. .
• HORSFIELD, Keith. Some mathematical properties of branching trees with application to the respiratory system. Bulletin of Mathematical Biology. 1976, s. 305–315. DOI 10.1007/BF02459562. PMID 1268383. .HORTON, R. E. Erosional development of streams and their drainage basins: hydro-physical approach to quantitative morphology. Geological Society of America Bulletin. 1945, s. 275–370. DOI 10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2. .
• LANFEAR, K. J. A fast algorithm for automatically computing Strahler stream order. Journal of the American Water Resources Association. 1990, s. 977–981. DOI 10.1111/j.1752-1688.1990.tb01432.x. Bibcode 1990JAWRA..26..977L. .
• LANGHAMMER, J. Vymezení typů vdních toků. Přírodovědecká fakulta Karlovy univerzity, Praha, 2009.
• LUTTENBERGER, Michael; SCHLUND, Maxmilian. An extension of Parikh’s theorem beyond idempotence. [s.l.]: [s.n.], 2011. Bibcode 2011arXiv1112.2864L. arXiv 1112.2864. 
• STRAHLER, A. N. Hypsometric (area-altitude) analysis of erosional topology. Geological Society of America Bulletin. 1952, s. 1117–1142. DOI 10.1130/0016-7606(1952)63[1117:HAAOET]2.0.CO;2. .
• STRAHLER, A. N. Quantitative analysis of watershed geomorphology. Transactions of the American Geophysical Union. 1957, s. 913–920. DOI 10.1029/tr038i006p00913. Bibcode 1957TrAGU..38..913S. .
• WAUGH, David. Geography, An Integrated Approach. 3rd. vyd. [s.l.]: Nelson Thornes, 2002. .