Lagrangeova interpolace

Příklad užití Lagrangeova polynomu pro interpolaci čtyř bodů

Chceme-li interpolovat funkci, která je dána svými hodnotami v $n+1$ bodech $x_{i}$, $i=0,1,...,n$ (body $x_{i}$ nazýváme uzly interpolace), a tedy požadujeme, aby hledaná funkce procházela zadanými body, můžeme použít interpolaci Lagrangeovým interpolačním polynomem. Interpolační funkce nám potom poslouží k získání polynomu procházejícím všemi body na intervalu $<x_{0},x_{n}>$.

Máme-li zadány hodnoty funkce $f$ v $n+1$ různých bodech, tzn. máme zadáno $n+1$ tzv. interpolačních podmínek pro polynom, je zřejmé, že stupeň hledaného polynomu bude $n$. Lze ukázat, že mezi všemi polynomy nejvýše $n$-tého stupně existuje právě jeden, který je interpolačním polynomem pro zadanou funkci. Pro určení interpolačního polynomu existuje několik postupů, ale je třeba si uvědomit, že pro zadanou funkci všechny postupy určí stejný polynom.

Langrangeův interpolační polynom je jedním ze známějších a také snadných způsobů interpolace funkce zadané pouze v diskrétních bodech. Nechť tedy máme dáno $n+1$ bodů, přes které funkce prochází. Pak můžeme pomocí rovnice popsané ve Wikiknihách nalézt interpolační funkci, která se původní rovnici snaží co nejvíce přiblížit.

Konstrukce Lagrangeova interpolačního polynomu

Známe-li $(n+1)$ uzlových bodů bodů $x_{0}\cdots x_{n}$ a jim odpovídající funkční hodnoty $f(x_{0})\cdots f(x_{n})$, sestavíme Lagrangeův interpolační polynom $L_{n}(x)$ n-tého řádu následovně:

$L_{n}(x)=P_{1}(x)+\cdots +P_{n}(x)=f(x_{0})\ell _{0}(x)+\cdots +f(x_{n})\ell _{n}(x)$,

kde $P_{i}(x)$ jsou pomocné polynomy a pro $\ell _{i}(x)$ platí:

$\ell _{i}(x_{j})={\begin{cases}1&{\text{pro }}i=j\\0&{\text{pro }}i\neq j\end{cases}}$

Tyto podmínky splňuje polynom:

$\ell _{i}(x)=\prod _{\begin{smallmatrix}0\leq m\leq n\\m\neq i\end{smallmatrix}}{\frac {x-x_{m}}{x_{i}-x_{m}}}={\frac {(x-x_{0})}{(x_{i}-x_{0})}}\cdots {\frac {(x-x_{i-1})}{(x_{i}-x_{i-1})}}{\frac {(x-x_{i+1})}{(x_{i}-x_{i+1})}}\cdots {\frac {(x-x_{n})}{(x_{i}-x_{n})}}$

Ukázka konstrukce interpolačního polynomu

Příklad Lagrangeova polynomu (popis zde)

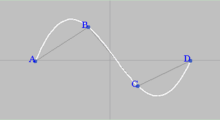
Obrázek vpravo ukazuje příklad konstrukce interpolačního polynomu $L_{3}(x)$. Známé body interpolované funkce $[x_{i},f(x_{i})]$, kde $i$ nabývá celočíselných hodnot od 0 do 3, nazýváme řídící body (barevné kružnice na obrázku). Cílem interpolace je, aby výsledná funkce (polynom) $L_{3}(x)$ procházela všemi řídícími body.

Pomocné polynomy $P_{i}(x)=f(x_{i})\ell _{i}(x)$ (barevné křivky na obrázku) prochází svými příslušnými řídícími body a v ostatních řídících bodech $[x_{j},f(x_{j})],(j\neq i)$ je jejich hodnota nulová. Lze je sestavit podle výše uvedených vzorců. Tedy:

$L_{3}(x)=f(x_{0}){\frac {(x-x_{1})}{(x_{0}-x_{1})}}{\frac {(x-x_{2})}{(x_{0}-x_{2})}}{\frac {(x-x_{3})}{(x_{0}-x_{3})}}+f(x_{1}){\frac {(x-x_{0})}{(x_{1}-x_{0})}}{\frac {(x-x_{2})}{(x_{1}-x_{2})}}{\frac {(x-x_{3})}{(x_{1}-x_{3})}}+$

$+f(x_{2}){\frac {(x-x_{0})}{(x_{2}-x_{0})}}{\frac {(x-x_{1})}{(x_{2}-x_{1})}}{\frac {(x-x_{3})}{(x_{2}-x_{3})}}+f(x_{3}){\frac {(x-x_{0})}{(x_{3}-x_{0})}}{\frac {(x-x_{1})}{(x_{3}-x_{1})}}{\frac {(x-x_{2})}{(x_{3}-x_{2})}}$

Součtem všech pomocných polynomů tak vzniká polynom procházející všemi řídícími body $L_{3}(x)$ (černá křivka na obrázku).

U polynomů vyšších řádů je výše popsaný postup časově náročný. Proto se využívá rovnosti $L_{n}(x)=a_{0}+a_{1}x^{1}+\cdots +a_{n}x^{n}=\sum _{i=0}^{n}a_{i}x^{i}=f(x)$ ke konstrukci matice $\Lambda$ typu $n\times n$, jejíž řádky reprezentují lagrangeův polynom n-tého stupně vyčíslený v bodech $[x_{i},f(x_{i})]$. Vektor pravých stran je identickým se sloupcovým vektorem ${\vec {f(x_{i})}}$.

$\Lambda ={\begin{pmatrix}a_{0}&a_{1}x_{1}&a_{2}x_{1}^{2}&\cdots &a_{n}x_{1}^{n}\\\vdots &\vdots &\vdots &\ddots &\vdots \\a_{0}&a_{1}x_{i}&a_{2}x_{i}^{2}&\cdots &a_{n}x_{i}^{n}\\\vdots &\vdots &\vdots &\ddots &\vdots \\a_{0}&a_{1}x_{2}&a_{2}x_{2}^{2}&\cdots &a_{n}x_{n}^{n}\\\end{pmatrix}}$

$,{\vec {f(x_{i})}}={\begin{pmatrix}f(x_{0})\\\vdots \\f(x_{i})\\\vdots \\f(x_{n})\\\end{pmatrix}}$

Neznámé konstanty $a_{0},a_{1},\cdots ,a_{n}$ pak nalezneme některou z metod řešení matic (např. Gaussovou eliminační metodou).

Související články

• Newtonova interpolace
• Polynom

Externí odkazy

• Lagrangeův interpolační polynom
• Lagrangeův interpolační polynom
• Fajmon, Růžičková - Matematika 3 (kapitola 6.1.2)