Devatenáctiúhelník

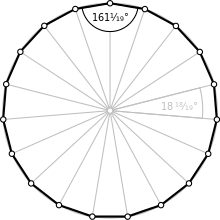
Devatenáctiúhelník, cizím slovem nonadecagon či enneadecagon (z řec. δεκαεννιά, dekaennia - devatenáct, a γωνία, gonia - úhel), je mnohoúhelník s devatenácti úhly, vrcholy a stranami.

Číselné údaje[editovat | editovat zdroj]

Součet středových úhlů je 180°, jeden středový (a zároveň vnější) úhel tedy musí být ${\frac {360^{\circ }}{19}}=18{\frac {18}{19}}^{\circ }\approx 18{,}9474^{\circ }$ . Následkem toho je jeden vnitřní úhel $180^{\circ }-18{,}9474^{\circ }\approx 161{,}0526^{\circ }$ , což lze též zapsat složeným zlomkem $161{\frac {1}{19}}^{\circ }$ . Součet vnitřních úhlů tedy bude $161{\frac {1}{19}}^{\circ }\cdot 19=3060^{\circ }$ .

Je-li α délka strany, pak:

Obvod: $P=19\,a$
Obsah: $A={\frac {19}{4}}\,a^{2}\cot \left({\frac {\pi }{19}}\right)$
Min. poloměr: $H={\frac {2\,A}{P}}={\frac {a}{2}}\cot \left({\frac {\pi }{19}}\right)$
Max. poloměr: $R={\frac {H}{\cos \left({\frac {\pi }{19}}\right)}}={\frac {a}{2\sin \left({\frac {\pi }{19}}\right)}}$

Rýsování[editovat | editovat zdroj]

Pravidelný devatenáctiúhelník nelze narýsovat pouze za pomoci pravítka a kružítka, neboť aby bylo možno daný pravidelný mnohoúhelník narýsovat, musí být všechny jeho liché dělitele být Fermatova čísla ( $F_{n}=2^{2^{\overset {n}{}}}+1$ ).

Devatenáct je dělitelné devatenácti, což je liché číslo a přitom není Fermanovo. S menší odchylkou (středový úhel se změní z $18{,}9474^{\circ }$ na $18{,}9246^{\circ }$ , odchylka tedy $0{,}0228^{\circ }$ a celkově $0{,}4332^{\circ }$ ) jej však lze zkonstruovat ve 14 krocích:

Narýsujeme přímku p.
Zkonstruujeme kružnici k s poloměrem r a se středem v bodě I, jež se nalézá na přímce p.
Sestrojíme kružnici l se středem v pravém průsečíku přímky p a kružnice k $J=p\cap k$ a má
Sestrojíme kružnici m se středem v levém průsečíku přímky p a kružnice k $K=p\cap k$ .
Utvoříme přímku q, jež protíná průsečíky kružnic l a m $L=l\cap m$ a $M=l\cap m$ .
Sestrojíme kružnici n, jež má poloměr r a střed v průsečíku J.
Vytvoříme kružnici o, jež má poloměr r a střed v horním průsečíku kružnice k s přímkou q $N=k\cap q$ .
Utvoříme přímku r, jež prochází průsečíky kružnice k s kružnicí n $O=k\cap n$ a $P=k\cap n$ .
Zkonstruujeme přímku s, jež prochází průsečíky kružnice k s kružnicí o $Q=k\cap o$ a $R=k\cap o$ .
Narýsujeme kružnici p se středem v průsečíku přímky p a s $S=p\cap s$ , jež prochází bodem I.
Narýsujeme kružnici q se středem v bodě I, jež prochází průsečíkem S.
Sestrojíme přímku t, jež spojuje průsečíky kružnic p a q $T=p\cap q$ a $U=p\cap q$ .
Zkonstruujeme přímku u, jež prochází průsečíkem K a průsečíkem přímek t a r $V=t\cap r$ .
Přímka u nyní svírá s přímkou p úhel α. Vzdálenost mezi jejich průsečíky s kružnicí k $V=u\cap k$ a $W=p\cap k$ nyní vezmeme do kružítka a po obvodu kružnice si uděláme značky, jež následně pospojujeme.