Teorie superstrun
Teorie strun, resp. teorie superstrun, je jedna z teorií aspirujících na tzv. teorii všeho. Teorie předpokládá, že základními stavebními kameny přírody nejsou bodové částice s nulovými rozměry, nýbrž jednorozměrné (otevřené resp. uzavřené) struny, které vibrují různými způsoby, odpovídajícími různým druhům elementárních částic. Veškeré interakce se redukují na spojování a rozpojování strun. Zastánci této dosud kontroverzní teorie se domnívají, že tato teorie elegantně a harmonicky sjednocuje teorie velkého a malého, tedy obecnou teorii relativity a kvantovou mechaniku, které jsou jinak neslučitelné. Podle teorie superstrun má vesmír – namísto známých čtyř rozměrů časoprostoru – rozměrů deset (tři pozorované prostorové rozměry, šest kompaktifikovaných nepozorovaných dodatečných prostorových rozměrů a jeden časový rozměr). Dodatečné rozměry jsou svinuty do variety malé velikosti (tzv. Planckovy délky), v důsledku čehož unikají přímému pozorování.
Historie[editovat | editovat zdroj]
Původní tzv. teorie strun z roku 1974 popisovala na základě Eulerovy Beta funkce pouze silnou interakci mezi kvarky prostřednictvím gluonů, ale během tzv. první superstrunové revoluce v roce 1984 se ukázalo, že tzv. teorie superstrun popisuje všechny dosud známé interakce včetně gravitace.
V současné době existuje pět konzistentních, ale vzájemně se lišících teorií superstrun. Tyto teorie jsou však díky supersymetrii pevně svázány dualitami, objevenými během tzv. druhé superstrunové revoluce v roce 1995. Pomocí těchto dualit a přidáním dalšího dodatečného prostorového rozměru sjednocuje tyto teorie tzv. M-teorie, která je formulována pro časoprostor o jedenácti dimenzích a zahrnuje i jedenáctidimenzionální supergravitaci. Mnoho vlastností M-teorie ale ještě čeká na vysvětlení.[1]
Přehled strunových teorií[editovat | editovat zdroj]
| Strunové teorie | ||
|---|---|---|
| Typ | Rozměry |
Detaily |
| Bosonová | 26 | Pouze bosony, žádné fermiony, to znamená pouze síly, žádná hmota, s otevřenými i uzavřenými strunami; hlavní chyba teorie: částice s imaginární hmotností, nazvané tachyony. |
| I | 10 | Supersymetrie mezi silami a hmotou, s otevřenými i uzavřenými strunami, žádné tachyony, grupová symetrie je SO(32) |
| IIA | 10 | Supersymetrie mezi silami a hmotou, pouze s uzavřenými strunami, žádné tachyony, nehmotné fermiony mají spin v obou směrech (nechirální) |
| IIB | 10 | Supersymetrie mezi silami a hmotou, pouze s uzavřenými strunami, žádné tachyony, nehmotné fermiony mají spin pouze v jednom směru (chirální) |
| HO | 10 | Supersymetrie mezi silami a hmotou, pouze s uzavřenými strunami, žádné tachyony, heterotická, význam strun pohybujících se vlevo a vpravo se liší, grupová symetrie je SO(32) |
| HE | 10 | Supersymetrie mezi silami a hmotou, pouze s uzavřenými strunami, žádné tachyony, heterotická, význam strun pohybujících se vlevo a vpravo se liší, grupová symetrie je E8×E8 |
Struny a blány[editovat | editovat zdroj]
-
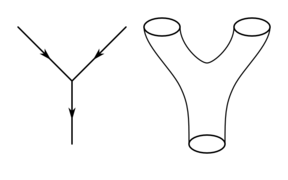
Feynmanův diagram (vlevo) převeden na strunový model (vpravo).
-
Feynmanův diagram (vlevo) převeden na strunový model (vpravo).
-
Model Frobeniovy věty.
-
Struny na anuloidu a na kouli.
Kromě jednorozměrných strun předpokládá teorie také existenci vícerozměrných útvarů, tzv. p-blán (membrán). Uzavřené struny mohou vibrovat buď volně na bláně anebo na blánu navinuté (viz struny na anuloidu). Konce otevřených strun se mohou pohybovat pouze po bláně.
Co teorie superstrun vysvětluje[editovat | editovat zdroj]
Experimentálně je známo, že elementární částice tzv. standardního modelu jsou uspořádány do tří rodin, navzájem odlišných pouze hmotností. Standardní model nemá pro toto žádné jednoznačné a teoreticky podložené vysvětlení. V teorii superstrun byl vysloven předpoklad, že tři rodiny elementárních částic by mohly souviset se základní topologickou charakteristikou geometrických objektů, která se nazývá genus. Intuitivně jde o počet otvorů v geometrickém objektu, kterým jsou tzv. Calabiho–Yauovy variety.
Superstrunová teorie by měla být teorií elementárních částic a mezi množinou zatím nepozorovaných částic je též teorií předpovězená nehmotná částice se spinem dva, tj. takové vlastnosti by měl mít graviton jakožto součást kvantové teorie gravitace.
Superstrunná teorie docílila určitého pokroku v práci se singularitami a divergencemi, umožňuje matematicky lépe popsat některé související teoretické představy, např. pro období krátce po velkém třesku nebo entropii černé díry.
Co teorie superstrun nevysvětluje[editovat | editovat zdroj]
Teorie superstrun, přinejmenším ve své současné podobě, má jen značně neurčitou a nejasnou formální i obsahovou strukturu (postuláty, rovnice, interpretace). Neumožňuje vypočíst hmotnosti elementárních částic, ani hodnoty těch vazebních konstant a parametrů, které figurují již ve standardním modelu. Nepodává žádný jasný a jednoznačný předpis pro tzv. kompaktifikaci, tedy problém, jak přejít z prostoru o předpokládaném vysokém počtu dimenzí (např. 11 nebo 27) do běžného čtyřrozměrného časoprostoru. Příslušných produktů kompaktifikace, tzv. Calabiho–Yauových variet, existuje pak nespočetně mnoho a není známo, na základě jakého dodatečného principu mezi nimi fyzikálně vybrat a docílit konkrétnější předpovědi. Tím, že teorie superstrun připouští v podstatě téměř libovolně vysoký počet nikdy nepozorovaných elementárních částic, neposkytuje ani určení toho, kolik elementárních částic vlastně existuje. Teorie superstrun dnes neumožňuje prakticky žádné testovatelné netriviální předpovědi v oblasti experimentálně dostupné fyziky. Nezanedbatelná část fyziků proto na teorii superstrun v její současné podobě pohlíží skepticky, anebo mnohá její tvrzení přímo odmítá.
Experimentální ověření[editovat | editovat zdroj]
Experimentální ověření teorie zatím neexistuje, určitým pokrokem by mohlo být uvedení do provozu LHC, který začal pracovat v září 2008. Fyzikové doufají, že by mohly být s jeho pomocí objeveny alespoň některé z mnoha supersymetrických částic, které teorie superstrun předpovídá. Protože však současné teorie superstrun připouštějí supersymetrických částic v podstatě neomezené množství, významnější verifikace teorie touto cestou je obtížná.
Další možností pro dílčí verifikaci teorie by mohlo být přímé pozorování obří superstruny ve vesmíru. Přesněji řečeno, nějakého geometrického útvaru, který by bylo možné interpretovat jako Calabiho–Yauovu varietu v teorii superstrun. Takováto superstruna by snad mohla vzniknout v raných fázích vesmíru a nyní by se mohla při pozorování jevit jako určitá gravitační čočka. Možnosti tohoto typu jsou ovšem dosud velmi nejasné a neprůkazné nejen na úrovni experimentu, ale i na úrovni interpretace, která je u teorie superstrun zatím málo rozpracovaná.
Odkazy[editovat | editovat zdroj]
Reference[editovat | editovat zdroj]
Literatura[editovat | editovat zdroj]
- Brian Greene: Elegantní vesmír. Superstruny, skryté rozměry a hledání finální teorie, Mladá fronta, Praha 2001, ISBN 80-204-0882-7
- Brian Greene: Struktura vesmíru - Čas, prostor a povaha reality, Paseka, Praha- Litomyšl 2006, ISBN 80-7185-720-3
- Stephen Hawking: Vesmír v kostce, ISBN 80-7203-421-9
- Michio Kaku: Paralelní světy – Putování stvořením, vyššími dimenzemi a budoucností vesmíru, ISBN 978-80-7203-847-3
- Michio Kaku: Hyperprostor – Vědecká odysea paralelními vesmíry, zakřiveným prostorem a desátým rozměrem, ISBN 978-80-257-0013-6
- Michio Kaku: Dále než Einstein. Hledání teorie vesmíru, ISBN 978-80-257-0142-3
- WOIT, Peter. Dokonce ani ne špatně. 1. vyd. [s.l.]: PASEKA, 2010. 336 s. (Fénix). Dostupné v archivu pořízeném dne 2014-07-14. ISBN 978-80-7432-029-3. Archivováno 14. 7. 2014 na Wayback Machine.